Цвета, которых не увидишь на экране
В глазу у человека есть три вида колбочек. В мониторах, цифровых фотоаппаратах, видеокамерах и сканерах свет попадает на фотоприемники через три разных светофильтра: красный, зеленый и синий. Почему именно такие цвета выбраны - ну очевидно неспроста, именно на них реагирует глаз, и смешивая их в разных пропорциях можно получить любой цвет, который человек вообще способен углядеть.
Долгое время я думал именно так и лишь пару лет назад узнал, что все сложнее, чем кажется. Колбочки в глазу человека имеют более хитрые спектральные чувствительности, и хотя разных типов колбочек всего три, не удастся найти такие три цвета, чтобы любые другие получались их смешиванием! Вот и монитор способен воспроизвести далеко не все цвета, которые может увидеть человек.
По понятной причине я не смогу показать вам эти цвета, но расскажу, на что они похожи и где их искать.
В основном, это оттенки насыщенного зеленого, с плавным переходом в синий, а также фиолетовый цвет. Что-то похожее на фиолетовый на компьютере есть, но это все же пурпурный или слабонасыщенный фиолетовый (к нему добавили много белого).
Наверху изображена полоса, максимально приближающаяся к спектру. В ней очень насыщенные цвета, но их на удивление мало, на большом протяжении цвет почти не меняется. Честно полученный спектр (с помощью монохроматора) так себя не ведет, он куда более разнообразный. Попробуем прибавить сюда немного белого - это уменьшит насыщенность, зато получится отобразить больше цветов. Сверху вниз мы все добавляем и добавляем белый, пока наконец не получаем линейку цветов, которую монитор способен отобразить без "округления".

(Можно щелкнуть, чтобы открыть 1280х1024)
Как видно, между зеленым и синим идет очень плавный переход, вот его-то, но в насыщенном виде, ни в одном цифровом устройстве вы не встретите, только в аналоговом мире.
Почему так получается, могу попробовать объяснить, это предмет веселой науки колориметрии, изучающей восприятие цвета человеком.
Самое сложное в этой науке то, что внутрь человека особенно не влезешь, и не только по этическим соображениям. Обработка зрительной информации начинается уже в самом глазу, перед фоточувствительными клетками расположен довольно толстый слой нейронов, являющихся по сути частью мозга. В природе есть много красивейших решений, да и сам глаз во многом "произведение искусства", но иногда бывают такие ляпы, что хоть стой, хоть падай. Прежде чем свет попадет на фоторецепторы, он проходит через те самые обрабатывающие нейроны, и гасится из-за них на несколько порядков! Если бы они стояли ЗА фоторецепторами, человек видел бы на небе звезды примерно до 12-й величины, а не до 6-й, не 9 тысяч на всем небосводе, а около 2 миллионов. Правда, сразу возникает мнение - днем было бы хреново, солнышко бы слепило, но не уверен - у сов глаз сделан совсем правильно, днем они действительно любят спать, но могут и проснуться и в таком случае видят без проблем ( пруф).
Ну так вот, как же можно сравнивать цветовые ощущения разных людей? Вдруг тот цвет который все воспринимают как зеленый, я воспринимаю как красный (и наоборот), но поскольку мне объяснили, что он называется зеленым, то и я сам его называю зеленым, хоть и вижу как красный) Вопрос скорее философский (можно много-много настрочить, а толку чуть), чем физический, поэтому народ придумал, как от этого уйти. Как сделать количественное описание цветов, не зная спектральные чувствительности рецепторов человеческого глаза.
Соображение первое: у нас всего 3 типа колбочек, это не обязательно как-то доказывать, можно просто принять как гипотезу и если удастся все цвета выразить 3 числами, значит она подтвердится. Так оно и вышло.
Второй важный факт: линейность восприятия. Если мы увидели свет одного спектра и восприняли его как цвет X, потом увидели свет другого спектра и восприняли его как цвет Y, то мы можем и не знать, что это за спектры такие, но их сумма даст цвет X+Y. Линейные пространства - это круто! Нам достаточно знать его размерность, а базис можно подобрать какой угодно.
Исторически решили за базис взять как раз-таки RGB, красный-зеленый-синий, а если точнее, то монохроматический свет с длинами волн 700нм для красного, 546.1нм для зеленого и 435.8нм для синего, последние - это ртутные линии.
Дальше поступили так: позвали кучу добровольцев (там не страшно, просто посмотреть на экранчик) и проецировали перед ними два пятна. Первое (условно, слева) - из монохроматора, свет определенной длины волны. Второй (справа) - сумма красного, синего и зеленого в пропорциях, долю каждого можно регулировать. От добровольцев требуется крикнуть, в какой момент они перестанут видеть границу между ними, цвета станут полностью совпадать, тем самым мы и найдем компоненты R,G,B данного монохроматического пучка. Поскольку любой свет - это сумма отдельных монохроматических компонент, то нам останется лишь с разными весами сложить R,G,B от каждой из компонент, и мы получим цвет любого наперед заданного пучка.
В ходе экспериментов обнаружилась странная вещь: чаще всего, чтобы уравнять два пятна, надо один из пучков R,G или B направить не на правую часть экрана, а на левую. Тогда мы приписываем этой компоненте знак минус. Линейное пространство обещает нам, что в любом базисе мы сможем решить задачу, но ничего не говорит о знаках. Вот что получается:

Не очень радостная картина, а что делать, нужно шагать дальше. Вспомнить, что мы не можем смешивать цвета с произвольными весами, а только с положительными (мы сейчас размышляем исключительно в терминах некогерентного света, у отдельных лучей складываются интенсивности, а они всегда положительные). Удобнее на этом этапе забыть об интенсивности света, из 3-х компонент R,G,B получить две цветовые:
r=R/(R+G+B) и g=G/(R+G+B). Тогда все цвета можно нарисовать на плоскости, в координатах r,g.
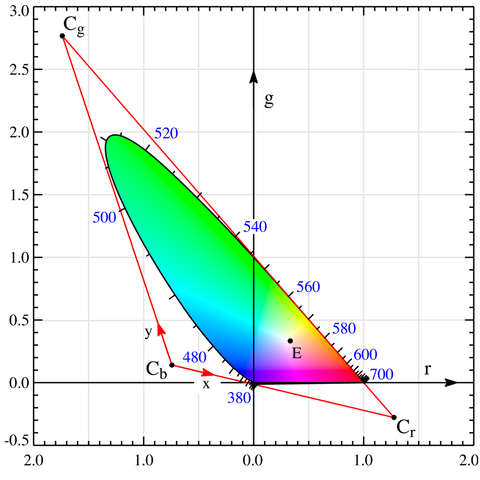
Хитрая дуга - это наш спектр. Чтобы смешать два цвета, нужно соединить их отрезком, все возможные сочетания будут лежать на нем. Если же мы начнем смешивать все чистые спектральные цвета, то неизбежно будем попадать внутрь замкнутой кривой, вмещающей в себя вообще все цвета, которые могут существовать.
Какие бы мы ни взяли три настоящих цвета (уже находяшихся внутри этой кривой или на ней), мы сможем получить из них лишь те цвета, которые расположены внутри треугольника, углы которых стоят на этих цветах, а это далеко не все имеющиеся, часть обязательно окажется вне его.
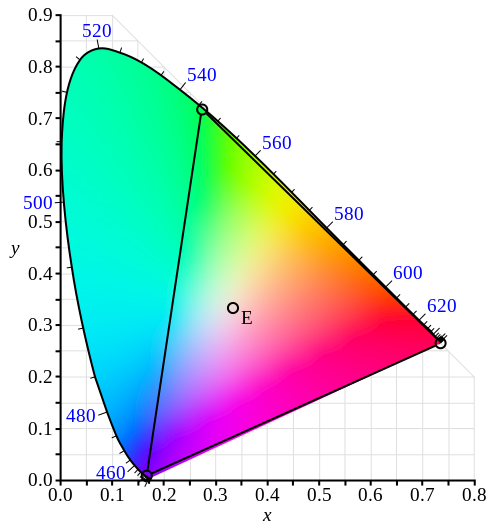
Здесь изображен треугольник, внутри которого все цвета, получаемые смешением R,G,B, тех самых, взятых за основу (здесь раскраска графика несет исключительно иллюстративную роль), вот мы и приходим к тому, с чего начинали: для полного счастья не хватает зелено-синих чистых цветов, они остались за бортом.
Подробности - у Фейнмана и еще в книге Теория и расчет светооптических систем.
Долгое время я думал именно так и лишь пару лет назад узнал, что все сложнее, чем кажется. Колбочки в глазу человека имеют более хитрые спектральные чувствительности, и хотя разных типов колбочек всего три, не удастся найти такие три цвета, чтобы любые другие получались их смешиванием! Вот и монитор способен воспроизвести далеко не все цвета, которые может увидеть человек.
По понятной причине я не смогу показать вам эти цвета, но расскажу, на что они похожи и где их искать.
В основном, это оттенки насыщенного зеленого, с плавным переходом в синий, а также фиолетовый цвет. Что-то похожее на фиолетовый на компьютере есть, но это все же пурпурный или слабонасыщенный фиолетовый (к нему добавили много белого).
Наверху изображена полоса, максимально приближающаяся к спектру. В ней очень насыщенные цвета, но их на удивление мало, на большом протяжении цвет почти не меняется. Честно полученный спектр (с помощью монохроматора) так себя не ведет, он куда более разнообразный. Попробуем прибавить сюда немного белого - это уменьшит насыщенность, зато получится отобразить больше цветов. Сверху вниз мы все добавляем и добавляем белый, пока наконец не получаем линейку цветов, которую монитор способен отобразить без "округления".

(Можно щелкнуть, чтобы открыть 1280х1024)
Как видно, между зеленым и синим идет очень плавный переход, вот его-то, но в насыщенном виде, ни в одном цифровом устройстве вы не встретите, только в аналоговом мире.
Почему так получается, могу попробовать объяснить, это предмет веселой науки колориметрии, изучающей восприятие цвета человеком.
Самое сложное в этой науке то, что внутрь человека особенно не влезешь, и не только по этическим соображениям. Обработка зрительной информации начинается уже в самом глазу, перед фоточувствительными клетками расположен довольно толстый слой нейронов, являющихся по сути частью мозга. В природе есть много красивейших решений, да и сам глаз во многом "произведение искусства", но иногда бывают такие ляпы, что хоть стой, хоть падай. Прежде чем свет попадет на фоторецепторы, он проходит через те самые обрабатывающие нейроны, и гасится из-за них на несколько порядков! Если бы они стояли ЗА фоторецепторами, человек видел бы на небе звезды примерно до 12-й величины, а не до 6-й, не 9 тысяч на всем небосводе, а около 2 миллионов. Правда, сразу возникает мнение - днем было бы хреново, солнышко бы слепило, но не уверен - у сов глаз сделан совсем правильно, днем они действительно любят спать, но могут и проснуться и в таком случае видят без проблем ( пруф).
Ну так вот, как же можно сравнивать цветовые ощущения разных людей? Вдруг тот цвет который все воспринимают как зеленый, я воспринимаю как красный (и наоборот), но поскольку мне объяснили, что он называется зеленым, то и я сам его называю зеленым, хоть и вижу как красный) Вопрос скорее философский (можно много-много настрочить, а толку чуть), чем физический, поэтому народ придумал, как от этого уйти. Как сделать количественное описание цветов, не зная спектральные чувствительности рецепторов человеческого глаза.
Соображение первое: у нас всего 3 типа колбочек, это не обязательно как-то доказывать, можно просто принять как гипотезу и если удастся все цвета выразить 3 числами, значит она подтвердится. Так оно и вышло.
Второй важный факт: линейность восприятия. Если мы увидели свет одного спектра и восприняли его как цвет X, потом увидели свет другого спектра и восприняли его как цвет Y, то мы можем и не знать, что это за спектры такие, но их сумма даст цвет X+Y. Линейные пространства - это круто! Нам достаточно знать его размерность, а базис можно подобрать какой угодно.
Исторически решили за базис взять как раз-таки RGB, красный-зеленый-синий, а если точнее, то монохроматический свет с длинами волн 700нм для красного, 546.1нм для зеленого и 435.8нм для синего, последние - это ртутные линии.
Дальше поступили так: позвали кучу добровольцев (там не страшно, просто посмотреть на экранчик) и проецировали перед ними два пятна. Первое (условно, слева) - из монохроматора, свет определенной длины волны. Второй (справа) - сумма красного, синего и зеленого в пропорциях, долю каждого можно регулировать. От добровольцев требуется крикнуть, в какой момент они перестанут видеть границу между ними, цвета станут полностью совпадать, тем самым мы и найдем компоненты R,G,B данного монохроматического пучка. Поскольку любой свет - это сумма отдельных монохроматических компонент, то нам останется лишь с разными весами сложить R,G,B от каждой из компонент, и мы получим цвет любого наперед заданного пучка.
В ходе экспериментов обнаружилась странная вещь: чаще всего, чтобы уравнять два пятна, надо один из пучков R,G или B направить не на правую часть экрана, а на левую. Тогда мы приписываем этой компоненте знак минус. Линейное пространство обещает нам, что в любом базисе мы сможем решить задачу, но ничего не говорит о знаках. Вот что получается:

Не очень радостная картина, а что делать, нужно шагать дальше. Вспомнить, что мы не можем смешивать цвета с произвольными весами, а только с положительными (мы сейчас размышляем исключительно в терминах некогерентного света, у отдельных лучей складываются интенсивности, а они всегда положительные). Удобнее на этом этапе забыть об интенсивности света, из 3-х компонент R,G,B получить две цветовые:
r=R/(R+G+B) и g=G/(R+G+B). Тогда все цвета можно нарисовать на плоскости, в координатах r,g.

Хитрая дуга - это наш спектр. Чтобы смешать два цвета, нужно соединить их отрезком, все возможные сочетания будут лежать на нем. Если же мы начнем смешивать все чистые спектральные цвета, то неизбежно будем попадать внутрь замкнутой кривой, вмещающей в себя вообще все цвета, которые могут существовать.
Какие бы мы ни взяли три настоящих цвета (уже находяшихся внутри этой кривой или на ней), мы сможем получить из них лишь те цвета, которые расположены внутри треугольника, углы которых стоят на этих цветах, а это далеко не все имеющиеся, часть обязательно окажется вне его.

Здесь изображен треугольник, внутри которого все цвета, получаемые смешением R,G,B, тех самых, взятых за основу (здесь раскраска графика несет исключительно иллюстративную роль), вот мы и приходим к тому, с чего начинали: для полного счастья не хватает зелено-синих чистых цветов, они остались за бортом.
Подробности - у Фейнмана и еще в книге Теория и расчет светооптических систем.