Friday Puzzle #38 - 2x2010 Sudoku
Near the start of this 2010 Project I responded to a comment by fellow Friday Puzzler Tom Collyer stating I had no plans to write any 2010-themed sudoku. My thinking at the time certainly included the fact that I'd already done a 2009 countdown sudoku that captured a good version of this kind of theme with a 9->1 thematic solve for December 31st. This construction demonstrated convincingly (to me) that 1->9 easy puzzles aren't that fundamentally interesting except as novelties since they are trivial to construct and trivial to solve (although maybe they belong as "example" puzzles in the very easy books).
But one aspect of that 2009 puzzle which keeps it from fitting in this series is that it is not truly symmetric. It has a kind of pseudosymmetry to where the 3x4 pixel numbers appear which almost counts. I cheated this way with my 2010 Slitherlink, but I'd rather at this point in the series stick to the letter of the design rules at play for the respective Nikoli puzzles particularly on a puzzle whose design rules are botched up so frequently. Let there be no doubt, since Nikoli is responsible for the term Sudoku, that their definition is that a valid 9x9 Sudoku puzzle must have 1) one answer, 2) no more than 32 or 33 givens, and 3) rotational symmetry of the givens.
The first principle is obvious and generally understood except in the published literature from time to time, such as when a bifurcation-based approach to search possible answer space is offered as a "proof" of how to solve any sudoku by a mathematician.
The second principle is a design concept possibly tied to a goal of giving at most 40% of the grid to a solver at the start. Contrast this standard to many of the first Number Place puzzles with ~36 givens, 4 per region, which were notoriously easy and may explain why the puzzle was relatively unnoticed in its many years in Dell magazines. In general, more elegant or more difficult sudoku will result from offering fewer givens to the solver. My quick check of Nikoli easy puzzles only revealed a max of 32 but I believe I've seen 33s so this is the range where I think Nikoli's set the bar, and it should be mentioned that the best Nikoli Easy sudoku don't even come close to having 32 or 33 givens because you can have an easy sudoku with far fewer.
On the third point, this is a mainly aesthetic goal but is common to many Nikoli puzzle types where the implementation of such a goal does not really limit the construction space for good puzzles. As a recommended adjustment to this requirement, I've seen (and written) nanpure published by other Japanese sources that allow for vertical, horizontal, or diagonal symmetry in place of rotational symmetry, opening up requirement 3 a bit for the hand-crafted nanpure community. But after searching through the ~500 print Sudoku I have from Nikoli with me at home (all solved, which makes the task harder to see just the given patterns), I could find no example of any puzzle lacking 180 degree rotational symmetry.* Thus, an equivalent 2010 theme to the earlier 2009 puzzle is flat out because it is against the last of the 3 main principles** of Nikoli Sudoku.
And of course Nikoli have never published, aside from some 9x9 latin square addition/multiplication puzzles (which are NOT sudoku even if WSCs can confuse them as such), anything close to a variation on the 1-9 digits in the 9x9 style besides their larger 16x16 and 25x25 forms (no "rectangular" 6x6 puzzles even). I like 007 sudoku as I've seen them called which use the digits {0,0,1-7} or sometimes 1-7 and two blanks since the repeated entry complicates eliminations in other cells for that entity. A 007-version of a 2010 theme is trivial to conceive and execute. It would probably make a more fun puzzle. But it would not be allowed by Nikoli so I will not do it for this series.
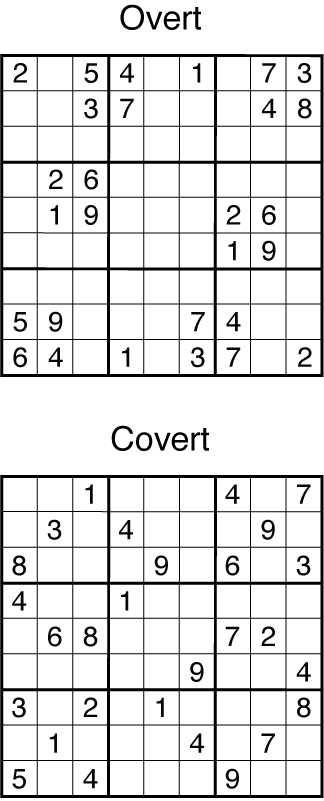
This leaves just a few possible themes in my mind, including a sort of symmetric digit/number hybrid as a possibility with 2 and 1 representing themselves and 2x2 squares of givens representing the 0's (or something similar with larger groups giving the 0 shapes), but this is much easier to achieve with a year like 2009 since the diagonally opposite 0's don't put the non-zero digits in the right place immediately. Its also possible to consider that there are some digits which are almost 0's. 2001 might be the best year for this type of theme, since a vertical 281 would look very much like a compressed 2001 theme and its easy to see how that could be set up in a grid. 6 and 9 are almost 0-like too, with extra tails on loops, so for the more open-minded in the crowd that is a second way I thought to directly theme a puzzle and you can see that at play in the overt puzzle as another duplicated element of theme in the center to go with the 2 0-shape 1 0-shape in the top/bottom. The more literal and closed-minded will say I've simply written a puzzle for 609 years in the future. At least 609 is rotationally symmetric for those still learning some of the rules here.
And so I've had the uninspiring but easy overt puzzle for awhile. And life (specifically my day job) intervened this week to make me think I could only post this simple puzzle, but then in framing this post I remembered how I used the 2009 puzzle to demystify a theme I see overused by sudoku constructors and so I wanted to write another 2010 puzzle to demystify a recent theme (not yet overused) from Nikoli.com that seemed to get a fair bit of chatter amongst those who noticed it but to me was particularly uninteresting since it felt trivial to accomplish. So, you get two puzzles. Hopefully something more entertaining or time-filling will be up here next week depending on your particular tastes.
* Having written this, I'm sure the first poster will point to multiple examples and conclude I'm an idiot who knows nothing about sudoku, which will make my next footnote moot.
** In my opinion, Nikoli has at least one more requirement: 4) a logical solution that can be discovered through application of a set of simple heuristics. These heuristics include naked/hidden singles, pairs, triples, (possibly quads), pointing pairs and box/line reduction. There is never anything more involved than that. Some solvers have used X-wings and the like to solve a Nikoli puzzle. I cannot immediately recall a puzzle that on further analysis REQUIRED that step, or coloring, or Y-wings, or worse. I've heard rumors (I believe from an interview I read long ago of Wayne Gould) of a puzzle that needed a Nishio but have never seen the puzzle and would say at best it is a huge exception to their body of work just like a mistake in a grid or answer key. I've also never carefully analyzed the 25x25 puzzles to see if exceptions exist there, but my experience suggests Nikoli has the logic capped at the level which still permits very elegant and challenging puzzles but without the more human-unfriendly steps. I would argue that the standard meaning of "Sudoku" should be exactly how Nikoli applies it in puzzle after puzzle when it appears in newspapers and books, and thus I hesitate to accept a 42-given puzzle with absolutely no symmetry in a Will Shortz book as a Sudoku for failing to use all the principles. To follow up on this point, it should go without saying that the fifth element of Nikoli sudoku is love. In other words, it was hand-crafted (or at the very least capable of convincing their editors that is was made in such a way). As my GAMES co-author selinker once said, without that human element, you just have "arrangements of ink."