Hashiwokakuro
No, that's not a typo but a subtle title combining hashi with kakuro. These are truly "Bridgesums", a variation that followed from discussion in my last post.
Rules:
Connect the islands with vertical and horizontal bridges so that all bridges are connected. Each bridge between islands will have (1 to n) lanes connecting them to other islands. The sum of the number of lanes leading off the island is given on each island. Just as in a kakuro, "lane numbers" do not repeat on an island. This means an island with the number 3 could have a single 3 lane bridge or a combination of a 1 and a 2 lane bridge, but not three 1 lane bridges.
The first puzzle and the example use (1 to 4) for the lane size, but the second (1 to 5) and third (1 to 6) puzzles use even wider superhighways. None are too hard, but increasing the possible sum space is useful to increase the potential difficulty.
Example:
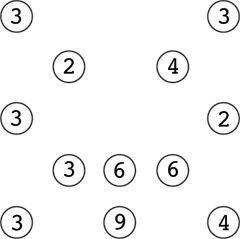
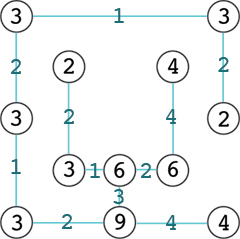
Solution:
Connect Four (1-4):

Johnny Five Is Alive! (1-5):

Six Degrees of Separation (1-6):

I'm not sure these are the huge improvement I was looking for although this variation has some variety to it.
Other ideas that really need to be done include hex islands (bridges go in one of 6 directions) but I don't have the graph paper or the photoshop grid file ready to power those out.
I could imagine adding black circles into the grid where the black circle represents a rock upon which a single bridge connects and makes a 90 degree turn. Enough black circles should create new logic.
Over-packing island space might change the dynamics of the puzzle - that I'm not sure about - but most puzzles are rather sparse. Maybe rules like no more than 3 islands can be connected in a line would change thinking too.
Anyway, I actually came up with a meta-puzzle idea involving a keystone and a checkerboard that is possibly useful on one of the above puzzles but may not be needed at all. I've not seen that in a bridges puzzle, but if you were trying to make a stone connection puzzle without any numbers at all this kind of embedding would be necessary.
Rules:
Connect the islands with vertical and horizontal bridges so that all bridges are connected. Each bridge between islands will have (1 to n) lanes connecting them to other islands. The sum of the number of lanes leading off the island is given on each island. Just as in a kakuro, "lane numbers" do not repeat on an island. This means an island with the number 3 could have a single 3 lane bridge or a combination of a 1 and a 2 lane bridge, but not three 1 lane bridges.
The first puzzle and the example use (1 to 4) for the lane size, but the second (1 to 5) and third (1 to 6) puzzles use even wider superhighways. None are too hard, but increasing the possible sum space is useful to increase the potential difficulty.
Example:

Solution:

Connect Four (1-4):

Johnny Five Is Alive! (1-5):

Six Degrees of Separation (1-6):

I'm not sure these are the huge improvement I was looking for although this variation has some variety to it.
Other ideas that really need to be done include hex islands (bridges go in one of 6 directions) but I don't have the graph paper or the photoshop grid file ready to power those out.
I could imagine adding black circles into the grid where the black circle represents a rock upon which a single bridge connects and makes a 90 degree turn. Enough black circles should create new logic.
Over-packing island space might change the dynamics of the puzzle - that I'm not sure about - but most puzzles are rather sparse. Maybe rules like no more than 3 islands can be connected in a line would change thinking too.
Anyway, I actually came up with a meta-puzzle idea involving a keystone and a checkerboard that is possibly useful on one of the above puzzles but may not be needed at all. I've not seen that in a bridges puzzle, but if you were trying to make a stone connection puzzle without any numbers at all this kind of embedding would be necessary.