Друзья и подруги, представляю вам круги!

[mark_y]

Тизер. Здесь вы прочтёте:
а) о русских, белорусских и украинских блогерах;
б) об удобном инструменте менеджмента;
в) демотиваторы.

Дисклеймер. Этот псто полон любви и обожания.
___________________________________________

Дудл сообщил о дне рождения славнейшего швейцарско-немецко-российского математика и механика. Имя ему Леонард Эйлер.




Моё знакомство с трудами выдающегося учёного состоялось на уроках дискретной математики, в частности алгебры логики. И эти уроки я не устаю вспоминать вот уже спустя более десяти лет. В том или ином виде они пригождаются в решении самых разных повседневных вопросов. Упражнения в математике в принципе прочищают голову, а тут ещё и пользы на вагон и маленькую тележку. Вы можете познакомиться со всем множеством (при упоминании учёного это слово начинает играть оттенками) явлений, названных в честь Эйлера (их тут более 50).

Одним из них, простым, но ловким инструментом, введённых в оборот гением математики, я хотел бы поделиться с теми, кто о нём ещё не слышал (вдруг пригодится!). Это круги Эйлера. Используются они не только в математике и логике, но и менеджменте, и в любых других сферах жизни, где нужно разобраться, что к чему.


На самом деле, любой пользователь интернета встречался с этими кругами, но не знал, что они так называются. Обычно эти круги используют в штуках. Вот несколько примеров.

1.


2.


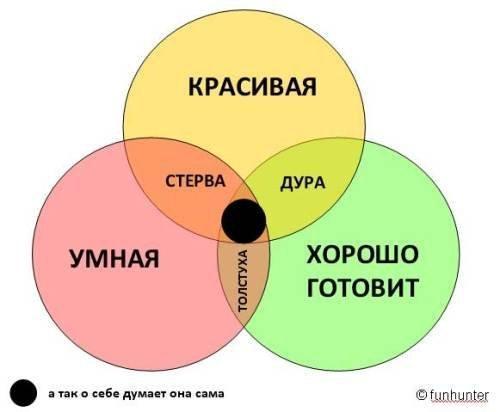
3.


4.


5.


6.


___________________________________________

А теперь к сути!

Всё (или практически всё) в жизни можно разделить на те или иные группы - другими словами, разбить множество на подмножества. Так, например, кириллических блогеров можно разделить на российских, украинских и т. д.

Бывает и так, что вещи ну никак не совмещаются между собой - иначе говоря, являются непересекающимися множествами. Например, (возьмём идеальную ситуацию) украинские блогеры не попадают в российский топ, а российские не лезут в украинский.

А бывает, что в каком-то месте такие группы пересекаются между собой, создавая новое подмножество, - например, российские блогеры, которые мухлюют: они приписывают себя к южным коллегам, чтобы попасть в украинский топ.

Можно рассмотреть и более сложные ситуации, но для начала нам хватит и этих.



Рис. 2

Леонард Эйлер придумал обозначать множества кругами.

Если элементы одного множества (назовём его множества В) полностью совпадают с элементами другого множества (для удобства назовём его множеством С), то мы нарисуем два круга с одинаковым диаметром и назовём его ВС. В нашем случае это, например, блогеры кириллического сегмента (множество В) и блогеры, имеющие дело с информацией, представленной кириллическими символами (множество С).

Если элементы множества А (украинские блогеры) совпадают с элементами множества В (кириллические блогеры), но элементы множества В имеют ещё и другие элементы, не относящиеся к множеству А, тогда мы говорим о том, что подмножество А входит в множество В. Тогда мы круг А помещаем в больший по размеру круг В (см. рис. 2.1).

Если у множеств А и В нет общих элементов (как в скорой будущей справедливой системе рейтингов ЖЖ), мы обозначаем это двумя кругами, которые не пересекаются между собой (см. рис. 2.2). Российские блогеры - отдельно, украинские блогеры - отдельно.

Если множество А и множество В имеют какое-то число общих элементов, мы говорим о том, что множества частично пересекаются. Образующееся подмножество элементов АВ обычно заштриховывается, а при необходимости получает своё наименование. Например, множество D - жулики. Но поскольку лайфхак священен, то будем говорить лишь о том, что некоторые элементы А относятся к множеству В. Графически изображаем, как круг А идёт внахлёст на круг В (см. рис. 2.3).

Закончить хочется с фанфарами. С восхвалением лучших чувств блогеров, ведущих честную игру. Если продолжать разбирать случай, когда часть элементов одного множества совпадает с частью элементов другого множества, мы невооружённым глазом обнаружим, что остаются элементы множества А, которые не совпадают с элементами В, и остаются элементы В, которые не совпадают с элементами А. Ничего общего с межнациональной рознью. Скорее вопрос рефрейминга (но это уже из другой лекции). Итак, мы можем заштриховать несовпадающие части круга, чем обратим внимание на элементы множеств, которые не имеют общих характеристик, и это рис. 2.4 (если представить, что области круг, где стоят буквы, заштрихованы).

Закрепим:



1. Множества совпадают.
2. Одно множество является подмножеством другого множества.
3. Множества могут пересекаться (тогда мы обсуждаем или область пересечения, или, напротив, непересекающиеся области).
4. То же яйцо, что и под п. 2, только в профиль. Раз мы говорим о том, что есть множество, которое является подмножеством, то в противоположном случае мы можем говорить о множестве, которое является надмножеством по отношению к множеству, которое в него заключено.
5. Множества не пересекаются.

___________________________________________

В качестве домашнего задания предлагаю разобрать шесть иллюстраций кругов Эйлера выше в терминах множеств. :)

Задание для тех, кто хочет усовершенствоваться в теме. Придумайте примеры для каждого представленного случая!



Всех с днём рождения Эйлера!

PS Кстати, вы знаете, что он владел множеством ;) европейских и древних языков. Отлично владел русским и даже писал на нём учебники.