The simple and easy single transistor NPN constant current sink for driving LEDs.
I constantly see people on Reddit /r/ece, /r/electronics, etc asking for advice on how to drive LEDs. It happens at least once a week. The classic approach is to take the input voltage, subtract the LED's forward voltage, and then use V = IR to compute the appropriate resistor. And that does work.
But there's another way. In my opinion, a better way. Better because it allows you to decide exactly how much current you want to run through the LED, and then build a very simple circuit that will keep the LED running at that current regardless of the voltage being applied to it. In other words, a constant current circuit.
There are lots of web pages showing you how to build a constant current circuit. Most of them, in my not very humble opinion, are stupidly overcomplicated. They insist on using multiple resistors, and consequently make both the math to calculate the resistor values and the wiring of the resulting circuit, way more of a hassle than it should be. Most of the time the extra complexity simply isn't worth it. So I'm going to tell you how to create a simple circuit that you can easily configure (one trivially computed resistor) that sinks a constant amount of current.
NOTE: I did not invent this circuit. I simply wish to popularize it, because I think it's better than most of the constant current circuits you'll find on the web.
Here it is:
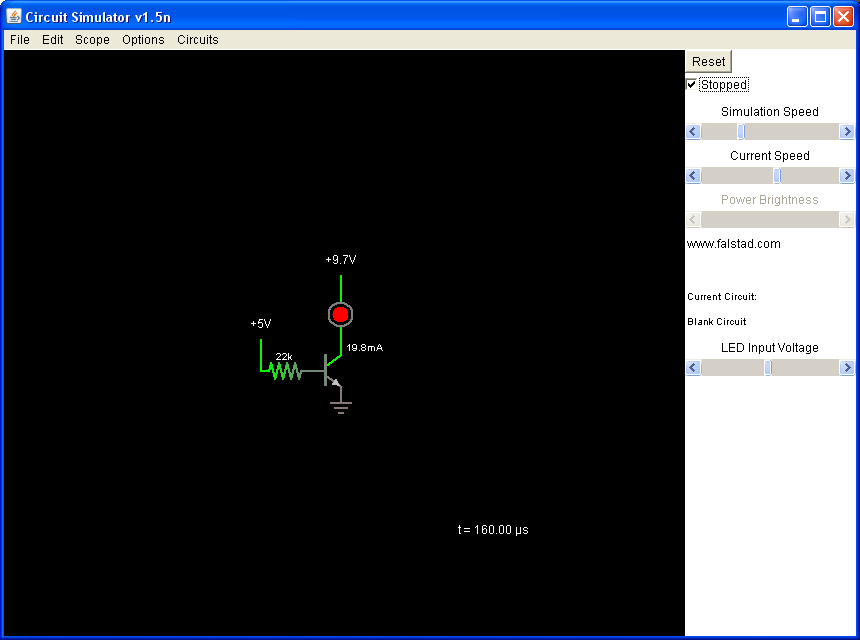
Click on the image to open circuit simulation in a new window/tab. (NOTE: Requires Java capable browser.)
Simple, no? The only thing you need to know is how to calculate the resistor. Here's the formula:
Rbase = 100 * ((Vconstant - 0.65) / Iconstant)
This circuit exploits two facts about an NPN transistor. First, an NPN transistor operating in forward active mode will have very close to a 650 mV differential voltage from base to emitter. Second, an NPN transistor's base to emitter current ratio ("beta" or "hFE") is generally about 100, and the transistor will dynamically alter its collecter-emitter resistance in an attempt to maintain that ratio.
To start, we connect the NPN's emitter straight to ground (by definition 0V). This guarantees that the voltage at the base of the transistor will be almost exactly 650 mV (0 V + 0.65 V = 0.65 V).
Now the constant voltage (Vconstant) comes into play. In this case the constant voltage is 5V, but the formula is exactly the same regardless of what the constant voltage is. So long as the voltage is constant, the circuit works. We attach a resistor from the constant voltage, to the base of the NPN. And now, because we know the voltages at both ends of the resistor, we can simply subtract them to find the effective voltage that the resistor "feels" across itself:
Voltage across Rbase = Vconstant - 0.65 V
At this point, we have to decide what we want our constant current (Iconstant) to be. For the purposes of this example, let's arbitrarily choose 20 mA, or 0.02 amps. Now we know both V and I, and so we can use them to compute R:
V = IR
V / I = R
R = (5 - 0.65) / 0.02
R = 217.5
This is the resistor value that will cause our constant current (Iconstant) to flow out of Vconstant and into the base of the NPN transistor.
However, remember that an NPN transistor has a current amplification ratio, or "beta". If we feed X amount of current into the base, then we get (X * beta) (usually, (X * 100)) current through the transistor's collector-emitter. We want our Iconstant to flow from emitter to collector. To make that happen, we need to have (Iconstant / beta) (usually (Iconstant / 100)) flowing into the base.
So we need to multiply the resistor value by 100. More resistance will mean less current. Specifically, 100 times more resistance will mean 100 times less current. But that's okay, because we turn right around and feed that current into the base of an NPN transistor. And the NPN transistor uses its "beta" to multiply the current by 100. And so we get back exactly the current we wanted, except now it's flowing through the collector of the NPN transistor. Right where we wanted it.
Rbase = R * 100
Rbase = 217.5 ohms * 100
Rbase = 21750 ohms
...or 21.75 kilo-ohms.
Now, 21.75k is not a standard resistor value. You could certainly create a 21.75k resistor by stringing together other standard value resistors in series. Say, two 10k resistors, a 1.2k, and a 560 ohm. 10k + 10k + 1.2k + 0.56k = 21.76k. This is not exactly 21.75k, but the error between 21.75k and 21.76k is only 0.046%. If you're using 10% tolerance resistors (and most standard resistors are 10% tolerance) the error inherent in your resistors because of their tolerances will be a couple orders of magnitude greater than the error between 21.75k and 21.76k.
But let's go a step further with this tolerance business. Note that 22k is a standard value resistor. Then do the math: the error between 21.75k and 22k is 1.15%. So if you're using 10% tolerance resistors, your 22k resistor might be 21.75k. Even if you're using fancy 1% resistors, 22k - 1% = 21.78k, which is quite nearly 21.75k. So, as long as you can afford for the current through your LED to be 1% less than you wanted, a 22k resistor (1% more resistance than you wanted) is fine.
So there you have it. A constant 5V fed through a 22k resistor into the 0.65V base of an NPN transistor, will result in 20 mA (- 1%) flowing through the NPN's collector. Now all we do is attach our LED to the collector of the NPN, and viola: we have a constant current LED driver!
And yes, I do mean constant current. It is the base-emitter voltage and the base current of an NPN that control collector current. So it does not matter what the voltage given to the LED is - there will be 20mA of current regardless. The NPN will dynamically adjust its resistance to ensure this. Because that is what bipolar transistors do: they dynamically adjust their collector to emitter resistance in an attempt to maintain the beta ratio between their base and collector currents.
In the simulation above, slide the "LED Input Voltage" slider back and forth. Notice that regardless of whether the voltage being fed to the LED is 3V or 17V, a constant 20mA (well, 19.8 mA, which is 20 mA - 1%) continues to flow through the LED. We control the NPN's base current, and therefore we control the collector current too. Jack up the collector voltage all you want, it doesn't matter. The NPN will not allow you to send more than 20mA (- 1%) through the collector.
(You can send less current into the collector if you like. The NPN will respond by lowering its collector-emitter voltage. Essentially attempting to lower its own resistance to the flow of current, trying to coax more current through the collector. Why? Because it's attempting to keep the ratio of base current and collector current constant. Because that is what bipolar transistors do.)
This constant current sinking behavior is especially useful for LEDs. The brightness of an LED is almost entirely controlled by the current flowing through it. A constant current driver means a constant brightness LED. Suppose you're powering an LED from batteries, whose voltage declines as they discharge. Say that you're using a lithium-ion battery that starts out at 4.2V at full charge, and declines all the way down to 3.6V when it's almost dead.
Now say you want to run an LED that requires 15 mA of current from this battery. Using the conventional "resistor in series with LED" logic, what value resistor do you use? Well, some people might say you want to make sure the LED doesn't burn out, so choose 4.2V as a worst case and compute your resistor accordingly: (4.2 - 2) / 0.015 = ~147 ohms. But now consider what happens when the battery is almost dead, and is only putting out 3.6V: (3.6 - 2) / 147 = 10.9 mA. We just lost about 30% of our LED current, and the LED will probably dim noticeably. Some people might call that a feature: dim LED indicates low battery. But if this is an LED headlamp or LED bike light... that might not be such a good thing.
Another scenario to consider: Suppose you have an LED, but you don't know what its forward voltage is. Yes, you can measure it with the diode test mode of your multi-meter. (Usually - some older meters can't measure the large voltage drops of newer white LEDs.) But what if the particular LED you measure is atypical, and most of the LEDs of that type have drastically higher or lower forward voltages? Well, why not just build a constant current sink? That way, regardless of what the LED's forward voltage is, the current is constant. No ifs, ands or buts. No worries about device variation. It just works. Constant current is constant.
This circuit is generally as brilliant as it is simple, but it does have one big gotcha. The nature of this circuit is that it dynamically adjusts the NPN transistor's resistance so as to ensure a constant current. At high input voltages, the transistor may be resisting a lot. So at high voltages, the power dissipation in the transistor can become large. Large enough that it can actually burn up the transistor.
You can get a very rough idea of what the power dissipation in the transistor is with a relatively simple formula:
P = I * V
Where P is power in watts, I is your constant current, and V is the input voltage. Note that "the input voltage" is reduced by the voltage drop of the LED.If you know the forward voltage drop of your LED, you can subtract it from the supply voltage before using the formula. If you don't know it, you can often use 2V as a safe estimate.
So, going back to the first example with 20 mA of current and a worst case input voltage of 17V:
P = IV
P = 0.02 * (17 - 2)
P = 0.3 watts
...or 300 mW. This is just over a quarter-watt (250 mW) and is generally safe for the kind of components that hobbiest electronics uses. (Though of course if you are in doubt, you should check the manufacturer's data sheet for the specific transistor you're using.)
Now consider another case: A fancy new high-power white LED with a voltage drop of 4V and a current of 200 mA.
P = IV
P = 0.2 * (17 - 4)
P = 2.6 watts
This is unsafe for TO-92 style transistors, and it is marginal even for the larger TO-220 style ones. So beware of high voltages! And always do your power calculation, just in case.
The other, relatively minor, weakness of this circuit is that it requires a constant voltage source. In practice, nearly all circuits have a voltage regulator - usually 5V - hanging around. So this is rarely a problem.
However, it is possible to use similar principles as shown above to create a relatively simple circuit that will maintain a constant current sink, without needing a constant voltage. Wanna know how? Click here! The cliff notes version: The LED current flows through a MOSFET and then through a resistor. The resistor develops a voltage difference proportional to the current running through it (by V = IR). The bottom of the resistor is grounded, and the top is attached to an NPN transistor's base. When the current rises too high, the voltage on the NPN's base rises above the 0.65 V threshold. The NPN then begins to conduct current through its collector-emitter. Said current is "stolen" from the gate of a MOSFET, which brings the gate voltage down, and so the MOSFET conducts slightly less current. And the MOSFET, remember, is what's controlling the current through the LEDs. It's a classic negative feedback system: too much current through the LEDs results in the gate voltage going down, reducing the LED current. Too little current has exactly the opposite effect. Very clever.
So there you have it. A simple 1-transistor, 1-resistor constant current sink. Go forth and ensure constant brightness! And plague me no more with your LED questions, you darn kids! GET OFF MY LAWN!