Regex matching: NFAs vs DFAs.
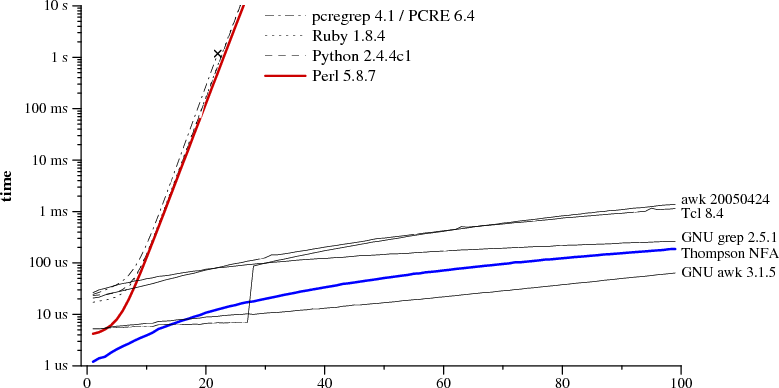
Notice that Perl requires over sixty seconds to match a 29-character string. The other approach, labeled Thompson NFA for reasons that will be explained later, requires twenty microseconds to match the string. That's not a typo. The Perl graph plots time in seconds, while the Thompson NFA graph plots time in microseconds: the Thompson NFA implementation is a million times faster than Perl when running on a miniscule 29-character string. The trends shown in the graph continue: the Thompson NFA handles a 100-character string in under 200 microseconds, while Perl would require over 1015 years. (Perl is only the most conspicuous example of a large number of popular programs that use the same algorithm; the above graph could have been Python, or PHP, or Ruby, or many other languages. A more detailed graph later in this article presents data for other implementations.)
It may be hard to believe the graphs: perhaps you've used Perl, and it never seemed like regular expression matching was particularly slow. Most of the time, in fact, regular expression matching in Perl is fast enough. As the graph shows, though, it is possible to write so-called "pathological" regular expressions that Perl matches very very slowly. In contrast, there are no regular expressions that are pathological for the Thompson NFA implementation. Seeing the two graphs side by side prompts the question, "why doesn't Perl use the Thompson NFA approach?" It can, it should, and that's what the rest of this article is about.
http://swtch.com/~rsc/regexp/regexp1.html
These aren't used much because the implementation is a little more difficult, and you have to give up some things, like backtracking. Still, if your program is limited by regex matching speed (most aren't, but just in case) you should consider using an NFA regex package, instead of the default DFA regexes that come with most languages/libraries.