Малые параметры больших катастроф

Был понедельник, день клонился к закату, стояла весна. Земля изобиловала зеленью и водами. Воздух Земли был сладок и дыханье утучняло, как сливки. Дожди, сходившие на Землю, были чисты, и эту чистоту можно было попробовать на вкус. У чистоты был освежающе-терпкий привкус. На Земле было тепло. Поверхность Земли шевелилась и вздымалась, не зная покоя от плодящейся жизни. Плодороднее всего Земля была в местах, где было больше трупов. Освежающе-терпкий дождик сеялся на зеленое поле, где трупов было очень много. Он падал на деревенское кладбище в Новом Свете. Кладбище было перенаселено - все промежутки между могилами покойников, умерших своей смертью, были забиты телами героев, погибших на войне. Марсиане (бывшие земляне) лежали бок о бок с нынешними землянами. На Земле в каждой стране были кладбища, где марсиане и земляне были погребены бок о бок. Не осталось ни одной страны на Земле, где не было сражений, когда вся Земля воевала с марсианами. Всё было прощено и забыто. Живые составляли единое Братство, а все мертвые - Братство еще более тесное (Курт Воннегут, «Сирены Титана»).
Мы привыкли к стабильности и постоянству. Мы ступаем по твердой поверхности Земли и верим, что она всегда будет служить нам опорой. Мы знаем, что вслед за зимой придет лето, станет тепло и солнечно, и так будет всегда. Мы думаем, что мир вокруг нас не может внезапно измениться, и, исходя из этого, формируем свой образ жизни и приоритеты, планируем свои действия.
Такая привычная, "бытовая" точка зрения на устойчивость нашего мира нашла свое отражение в науке XVIII века, когда создавалось классическое естествознание. Его основой стал математический язык дифференциального и интегрального исчислений; считалось, что все зависимости можно описывать непрерывными функциями, для которых характерно небольшое изменение значения функции при малых приращениях аргументов. Казалось бы, логично: приложено чуть больше усилий - получен чуть больший результат... Более того, если математические модели не отвечали этим условиям, то они считались некорректными, а значит, лишенными реального содержания.
Но... Легкий поворот выключателя приводит в действие управляющие механизмы, и открываются створки плотины, мощные потоки воды обрушиваются на лопатки турбин, заставляя крутиться многотонный вал генератора. Легкий удар по детонатору вызывает взрыв, при котором мгновенно высвобождается энергия, сравнимая с энергией маленького солнца. Есть примеры и нерукотворных природных процессов, когда в результате слабого воздействия пробуждаются силы, во много раз более мощные: маленький камешек может вызвать горный обвал, страшную по своим последствиям снежную лавину и даже землетрясение. Научная и инженерная мысль открыла множество примеров скачкообразного изменения системы при малых воздействиях, но, как ни странно, на наши представления об окружающем мире до недавнего времени это почти не влияло.
Еще в древности, например в античной Греции, среди философов существовало представление, что вся природа живет и развивается благодаря соразмерности и гармонии величайших сил - противоположностей, находящихся в равновесии. Нарушение этого равновесия может разрушить весь мир. За гармонию противоположностей отвечают боги, и они прикладывают немалые усилия для ее сохранения. Вспомним миф о Фаэтоне, который упросил своего отца Гелиоса дать ему небесную колесницу в доказательство его божественного происхождения. Руки смертного не удержали небесных коней, он не сумел провести колесницу по безопасному пути, где солнечные лучи не опаляют землю, но и не дают ей замерзнуть. Последствия не заставили себя ждать:
Трещины почва дала, и в Тартар
проник через щели
Свет, и подземных царя с супругою
в ужас приводит.
Море сжимается.
Вот уж песчаная ныне равнина,
Где было море вчера;
покрытые раньше водою
Горы встают...
(Овидий. Метаморфозы.)
Чтобы вернуть мир из хаоса, потребовалось вмешательство верховного божества Зевса, восстановившего порядок.
Древние философы понимали, что даже малые изменения, нарушающие гармонию, могут существенно изменить мир, ввергнуть его в хаос. Многие столетия их внимание занимали именно законы этой гармонии, так как в ней они видели проявление божественной воли, удерживающей мир в порядке. Начиная с пифагорейцев, открывших, что эти законы могут быть записаны на языке цифр и геометрических фигур, математику стали использовать как средство отражения идеальных законов природы, в которой все противоположности соразмерны и уравновешены. Может быть, этим и объясняется упорное нежелание "классических" математиков рассматривать неустойчивые математические модели, в которых возможно резкое нарушение равновесия.
Лишь в ХХ веке появились работы, в которых всерьез заговорили о том, что такие неустойчивости столь же реальны, как и состояния гармонии. Было осознано, что любая система, развиваясь, проходит этапы «перестройки», - резкого изменения, во время которых происходит перегруппировка сил, переустройство равновесия.

Пример "перестройки" в системе при участии скрытых сил
Эти этапы характеризуются временным преобладанием одной из сил, что приводит к хаосу, разрушающему предыдущие структуры; затем происходит гармонизация, равновесие восстанавливается, но уже в новом, качественно ином состоянии.
Одной из математических теорий, описывающих резкие переходы, является теория катастроф. Как научная дисциплина она появилась в 70-х годах прошедшего века. Важным достоинством этой теории является то, что она не требует подробных математических моделей и может описывать ситуации не "количественно", а "качественно", а ее результаты и выводы иллюстрируются простыми геометрическими образами.
В прошлом веке математику делили на чистую - равно применимую к окуркам и паровозам - и прикладную, то есть специально приспособленную к паровозам. А сравнительно недавно, когда потребовалось перейти от паровозов к атомам, самолётам и спутникам, вдруг оказалось, что чистая - «окурочная» - математика с её необычными объектами, такими, как представления групп, комплексные многообразия, многомерные пространства, и довольно-таки отвлечёнными разделами вроде топологии или функционального анализа гораздо лучше приспособлена к новым задачам, чем созданная для чисто практических нужд «паровозная».
А какова же по этой классификации теория катастроф, к чему она ближе, к чистой математике или прикладной?
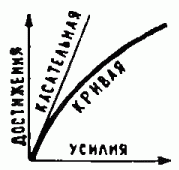
Рис. 1. В законе «Достижения пропорциональны усилиям» отражается фундаментальный принцип математического анализа: всякая гладкая функция в малом (то есть при малых приращениях аргумента) приближённо линейна.
Оказывается, что математическим источником теории катастроф служит сравнительно молодой раздел чистой, «настоящей» математики, который называется теорией особенностей гладких отображений. Фактически теория особенностей - смелое обобщение исследования функций на максимумы и минимумы. Почему такое исследование необходимо? Дело в том, что минимумы и максимумы представляют собой критические точки функции, которые во многом определяют её поведение. Известный французский математик Поль Монтель выразил это так: «Функции, как и живые существа, характеризуются своими особенностями». А чтобы понять, как именно, нам придётся рассмотреть несколько типичных примеров.
Современник Ньютона, английский учёный Гук, установил следующий закон, справедливый для упругих тел: удлинение такого тела, например, обычной пружины, почти пропорционально приложенной силе, пока она мала. (Это утверждение впоследствии так и назвали - законом Гука.) Точно так же в нормальных рыночных экономических условиях приращение спроса пропорционально малому уменьшению цены. И вообще очень часто достигаемый эффект оказывается пропорциональным затраченным усилиям. Однако нужно иметь в виду, что это верно лишь при малых приращениях, как часто говорят, локально (скажем, нынешнее уменьшение потребления алкоголя вряд ли пропорционально повышению цены на водку).
Приведённые примеры отражают один из универсальных законов:
I. В окрестности некритической точки приращение функции почти пропорционально приращению аргумента. Фактически этот закон отражает основной принцип классического математического анализа - любая гладкая, то есть не имеющая изломов и «клювиков», функция на малых участках (как говорят, в малом) приближённо линейна. Иными словами, гладкую кривую можно заменить её касательной (рис. 1). С простейшими универсальными законами такого рода мы встречаемся так часто, что уже перестали им удивляться. Но как прийти к пониманию этих законов, «прочувствовать» их? Так вот, оказывается, что исследование зависимости всевозможных математических объектов от определяющих их параметров и приводит к универсальным законам. Именно в этом, по существу, основной вывод математической теории особенностей.
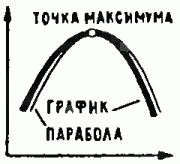
Рис. 2. Универсальный закон квадратичности: в окрестности точек максимума или минимума приращения функции (соответственно отрицательное или положительное) приблизительно пропорционально квадрату приращения аргумента.
Если рассматривать функцию не локально, то есть не на малом участке, а в целом, то она может быть и сильно нелинейной, например, иметь максимумы и минимумы. В окрестности точки максимума или минимума график типичной функции можно приближённо заменить параболой (рис. 2). Отсюда следует универсальный закон:
Во всех рассмотренных ситуациях речь идёт об универсальных законах, которые выполняются для любых гладких объектов (функций, кривых, поверхностей), за исключением лишь некоторых специальных, «нетипичных». Интересно, что такие, казалось бы, простые объекты, как плоскость и цилиндр,- нетипичные поверхности.
Теперь мы, пожалуй, уже готовы к тому, чтобы понять, что имеют в виду математики, произнося слово «катастрофа». Правда, вначале нам придётся сделать ещё одно небольшое математическое усилие. Представим себе кубическую зависимость - функцию у = х3 (рис. 6). В нуле она имеет «нетипичную» кубическую особенность. Но если задана не индивидуальная функция, а целое семейство функций, зависящих ещё от некоторого параметра, то оказывается, что существует такое значение параметра, при котором кубическая особенность становится устойчивой. Слово «устойчивость» здесь означает, что во всяком близком семействе при некотором близком значении параметра встретится точно такая же особенность.
Универсальный пример такого семейства- множество кубических функций у = х3+рх переменной х, зависящих к тому же от параметра р. Вид графика таких функций при разных значениях параметра показан на рис. 7.
Пока параметр р отрицателен, функция имеет вблизи нуля локальные максимум и минимум. Когда параметр р стремится к нулю, максимум и минимум сближаются, и при нулевом значении параметра возникает кубическая особенность. При положительных значениях параметра и максимум, и минимум исчезают, «убив» друг друга. Все эти явления универсальны и устойчивы, они наблюдаются и в семействах, близких к рассматриваемому. Поэтому такие явления имеют широкую область применимости.
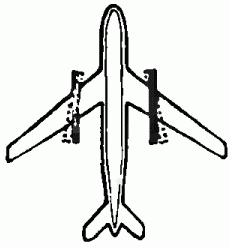
Рис. 3. Как спасти хвостовое оперение реактивного самолёта от струи раскалённых газов? Небольшое отклонение значения аргумента от оптимального практически не сказывается на значении функции. В частности, малый поворот реактивных двигателей не меняет результирующую силу тяги.
Пусть, например, наша функция характеризует состояние экономики (скажем, величину дохода диктатора и его приближённых) в зависимости от какого-либо параметра. (В качестве такого параметра можно взять, к примеру, правдивость информации.) Если экономика регулируется так, чтобы обеспечивать максимизацию функции, то система будет находиться в точке максимума. А до тех пор, пока с изменением дополнительного параметра этот максимум - локальный оптимум - не исчезнет.
В этот момент система будет вынуждена скачком перейти в далёкое от исходного состояние В (рис. 8). Такого рода перескоки и получили название катастроф, так как они связаны с резкими изменениями в состоянии системы и могут приводить к её разрушению.
Если бы мы не ограничивались узкими рамками малых изменений вблизи рассматриваемого локального оптимума, то картина могла бы быть, например, такой. Вначале оптимальное решение единственно (А на рис. 9). По мере развития системы возникает побочный максимум В - новый локально-оптимальный, но вообще-то не наилучший режим. Он рождается вместе с близким локальным минимумом. Кстати, это явление рождения двух экстремумов описывается таким же универсальным законом, как и изображённое на рис. 7 их взаимное уничтожение, меняется только направление изменения параметра. Далее, побочный максимум обгоняет исходный (С). Начиная с этого момента, новый режим уже выгоднее старого. Но переход на него затруднён необходимостью резкого перескока - катастрофы. Отсюда вытекает правило:
V. При плавном переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.

Рис. 4. Типичная кривая не имеет тройных касательных. При этом касание в двух точках устойчиво» то есть не исчезает при малом шевелении кривой.
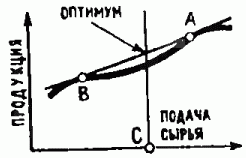
Рис. 5. Выбор пульсирующего оптимального режима. Предположим, что зависимость скорости выпуска продукции каким-либо производством (например, мельницей) от скорости подачи сырья изображается невыпуклой кривой. Как организовать работу, чтобы суммарный выход продукции при заданной средней скорости С подачи сырья (то есть при заданном расходе сырья за большое время) был максимальным?
Оказывается, оптимальный режим - пульсирующий: он составляется из чередующихся периодов интенсивной загрузки сырья (точка А) и слабой загрузки (точка В). Действительно, требуется так распределить массы по кривой, изображённой на рисунке, чтобы центр тяжести лежал над точкой С и находился возможно выше. Такое распределение масс сосредоточено в двух точках А и В касания кривой с прямой.
Оптимальный режим составляется из смеси двух, а не большего числа режимов, именно потому, что прямая касается типичной кривой не более чем в двух точках (см. рис. 4.).
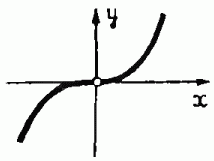
Рис. 6. График функции у=х3. Эта функция имеет при х=0 нетипичную, кубическую особенность.
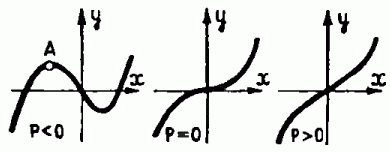
Рис. 7. Универсальная деформация кубической особенности. При возрастании параметра максимум и минимум функции сближаются и в конце концов исчезают, «убив» друг друга.
В линейных системах малое изменение параметра в сторону лучшего режима улучшает положение. В отличие от этого, после достижения локального оптимума малые изменения управляющего параметра, направленные в сторону лучшего режима, не улучшают, а ухудшают положение. И если, как это обычно бывает, система сама стремится локально оптимизировать своё состояние, то она будет отвечать на недостаточно радикальные изменения возникновением сильных тенденций возврата к старому режиму. Этим, думается, можно объяснить неудачу многих реформ, в частности экономических.
В живой природе аналогичная трудность, например, необходимость полной перестройки организма гусеницы для образования бабочки преодолевается при помощи специальной стадии - куколки. В этом случае отжившая система (гусеница) сама создаёт в своих недрах новую систему, которая впоследствии уничтожает старую (куколка в конце питается остатками гусеницы).
Наконец, в ходе дальнейшего развития системы исходное локально-оптимальное состояние вообще исчезает (D) и переход на далёкий от первоначального режим становится неизбежным (Е).
Универсальный закон (рис. 7) приводит к выводу:
VI. Расстояние от исчезающего локально-оптимального режима до движущегося ему навстречу локально-минимального - порядка квадратного корня из отличия параметра от катастрофического значения. Поэтому в момент катастрофы оба режима сближаются с бесконечной скоростью. Это, кстати, объясняет, почему так трудно бороться с грозящей катастрофой, когда её признаки сделались уже заметными.
Описанный сценарий оказывается лишь одной из возможных последовательностей локальных метаморфоз, качественных перестроек, или, как выражаются математики, бифуркаций. Все возможные сценарии взаимодействия двух локально-оптимальных режимов даются, как выяснилось, универсальным законом
у = х4 + ах2 + bх
с параметрами a и b. На рис. 10 изображён график экстремального значения у как функции параметров a и b.

Рис. 8. Катастрофическое изменение режима. Модели, основанные на представлениях теории катастроф» некоторые авторы пробуют применять и социальным системам и экономке.

Рис. 9. Сценарий глобальных перестроек в развивающейся системе. При плановом переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.
Сценарий, описанный выше, изображается на этом графике путём I, заканчивающимся катастрофическим скачком. Однако к той же самой конечной цели можно прийти без катастрофы, даже зайдя уже достаточно далеко по катастрофическому пути. Для этого надо вернуться назад и обойти разделяющую конкурирующие режимы точку с другой стороны (путь II).
Поверхность, изображённая на рис. 10, называется «ласточкиным хвостом». Она постоянно встречается в теории особенностей в качестве универсальной модели. Например, такие же «ласточкины хвосты» имеют фронты типичных воли, распространяющихся в трёхмерном пространстве. В местах особенностей волны особенно сильны. Именно этими особенностями объясняются, в частности, радуга на небе и разрушительная ударная волна от сверхзвукового самолёта.
Универсальных законов, подобных приведённым выше, оказалось не так уж много (хотя число их, конечно, растёт с увеличением числа переменных и параметров). Кроме ласточкиного хвоста в трёхмерном пространстве, особенно часто встречается ещё зонтик Уитни-Кэли (рис. 11) - поверхность, заданная уравнением у2 = zx2. Зонтиком эта поверхность называется потому, что, кроме нарисованной на рис. 11 поверхности, выписанному уравнению удовлетворяет и отрицательная часть оси z - своего рода «ручка» зонтика.
Если объекты нашего исследования характеризуются двумя параметрами, а мы, не зная их, измеряем три характеристики объекта и изображаем результат измерений точкой трёхмерного пространства, то полученные точки расположатся на некоторой поверхности. И вот оказывается, что, несмотря на полную гладкость зависимости измеряемых характеристик от параметров объекта, получающаяся поверхность, вообще говоря, имеет особенности, а именно зонтики, локально устроенные так, как указано на рис. 11.
Характерная особенность образуется при проектировании гладкой поверхности общего положения на плоскость.
Если соединить графики функций рис. 7 в одну поверхность (рис. 12) и спроектировать эту поверхность на плоскость (p, y) вдоль оси х, то видимый контур поверхности будет иметь остриё (точки возврата). На самой поверхности в этом месте нет никакой особенности. Особенность имеет лишь проектирование. При изменении направления проектирования особенность перемещается по поверхности. Эта особенность называется «сборкой Уитни».
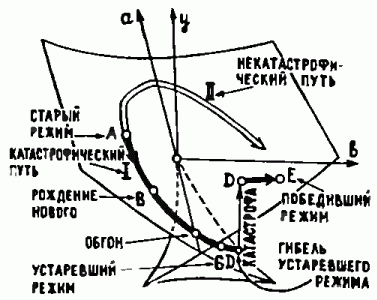
Рис. 10. Ласточкин хвост: универсальный закон зависимости оптимальных значений от параметров.
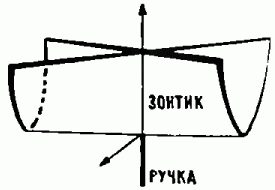
Рис. 11. Зонтик Уитни - Кэли. Зонтиком эта поверхность называется потому, что уравнению, задающему поверхность, удовлетворяет и отрицательная часть оси Z - своего рода «ручка» зонтика.
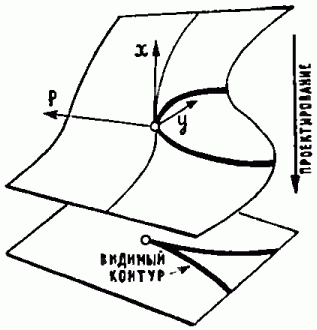
Рис. 12. Сборка Уитни: универсальный закон, в соответствии с которым изменяется внутреннее состояние системы в зависимости от параметров.
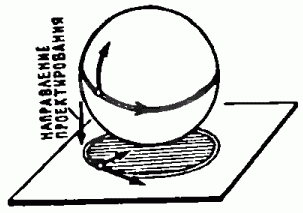
Рис. 13. Особенность, называемая складкой, возникает, в частности, при проектировании сферы на плоскость в точках экватора.
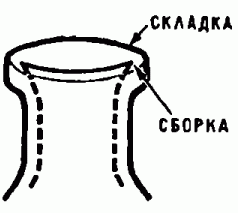
Рис. 14. Экспериментальное наблюдение сборки Уитни. На поверхности бутылки можно увидеть две сборки. Они устойчивы, в чём можно убедиться, покачивая бутылку.
В 1955 году американский математик Хасслер Уитни опубликовал работу «Об отображениях плоскости на плоскость». Фактически именно эта работа и заложила основу теории особенностей гладких отображений, а с ней - и теории катастроф. Отображение поверхности на плоскость - это сопоставление каждой точке поверхности точки плоскости. Уитни заметил, что в случаях «общего положения», то есть во всех случаях, кроме некоторых исключительных, встречаются особенности лишь двух видов - все другие разрушаются при малом «шевелении» тел или направлений проектирования, тогда как эти два вида особенностей устойчивы и сохраняются при малых деформациях отображения.
Сборка - одна из таких особенностей, вторую особенность Уитни назвал складкой, она возникает, если проектировать сферу на плоскость в точках экватора (рис. 13). Две сборки можно увидеть на поверхности бутылки (предпочтительнее из-под молока, рис. 14). Покачивая бутылку, мы экспериментально убеждаемся в том, что сборка устойчива. И вообще, отображения гладких поверхностей на плоскость окружают нас со всех сторон. Действительно, большинство окружающих нас тел ограничено гладкими поверхностями, при этом видимые контуры тел - проекции поверхностей, ограничивающих тела, на сетчатку глаза. Приглядываясь к окружающим нас телам, например, к лицам людей, мы можем изучить особенности видимых контуров. Например, точки сборки можно увидеть в чертах окружающих нас лиц там, где линия контура «исчезает» (рис. 15). Если применительно к человеческим лицам говорить на геометрическом языке, то можно заметить, что линия контура имеет касательную вплоть до точки сборки, но с приближением к этой точке кривизна линии растёт до бесконечности.
Теорема Уитни стала прообразом многочисленных универсальных законов строения особенностей, открытых в последующие годы. Простейшие из этих законов были уже известны в конкретных примерах специалистам в соответствующих областях. Историки науки недавно подметили, что до появления теории особенностей открытия этого рода особенно часто встречались в работах, удостоенных Нобелевской премии. Положение здесь такое же, как с математическим анализом: Гюйгенс решал без его помощи практически все задачи, решаемые Ньютоном и Лейбницем с помощью анализа, но для этого нужно было иметь гений Гюйгенса. Теперь же такие задачи благодаря анализу легко решает любой студент. Точно так же теория особенностей сделала легкодоступным тонкое искусство построения правильных моделей явлений, когда отбрасываются большие, но «физически несущественные» величины и сохраняются меньшие, но «физически важные» члены.

Рис. 15. Складки и сборки на лице Мики Морозова (портрет Валентина Серова).
Из предшественников теории особенностей можно отметить Гюйгенса (теория эволют и эвольвент), Гамильтона (теория систем лучей), Кэли (зонтики, фронты и каустики), Пуанкаре (теория бифуркаций, включая - катастрофисты обычно этого не знают - построение «версальных деформаций»), А. А. Андронова (структурная устойчивость, бифуркации аттракторов), Максвелла (фазовые переходы), Гиббса (правило фаз), Н. Н. Семёнова (тепловой взрыв), Я. Б. Зельдовича (теория горения и космология), Пирси (волновая оптика), Койтера (теория упругости), Л. Д. Ландау (фазовые переходы второго рода) и т. д.
Понимание того, что в основе всех этих (и многих других) исследований лежит одна и та же математическая структура, пришло не сразу, но когда это было осознано, то прогресс в каждой из перечисленных областей начал немедленно приводить к продвижениям во всех остальных. В настоящее время теория особенностей, бифуркаций и катастроф - один из наиболее бурно развивающихся отделов математики.
Сегодня на уровне математической теории можно утверждать, что любая достаточно сложная система, взаимодействующая со своим окружением, проходит в своем развитии определенные этапы. Вначале из неупорядоченных частей системы вдруг складываются и с колоссальной скоростью начинают расти множество структур - "новых форм". За счет противоположной, "разрушительной" тенденции скорость роста постепенно замедляется, некоторые формы исчезают, другие приобретают устойчивость. Эта тенденция рано или поздно одерживает верх, погружая все в изначальный хаос, и наступает кризис, порождающий структуры следующего этапа.
Таким образом, математическая модель развития совпадает с мифологической: согласно воззрениям Древней Индии, бог Брахма творит мир, упорядочивая хаос, а Шива разрушает его. В промежутках между двумя рождениями мир устойчив благодаря уравновешивающему началу - богу Вишну. В античных мифах порождающее божество Дионис выхватывает из хаоса бессчетное множество форм, а гармонизирующее начало - Аполлон - уравновешивает его взрывную творческую энергию, успокаивает бешеный рост форм, придает миру соразмерность. Нарушение гармонии - конфликт, необходимый для развития, - погружает систему в животворящий хаос, дающий ростки новой жизни.
Хаос - неизбежный, обязательный атрибут жизни любой достаточно сложной системы. Геометрическим образом хаоса может служить запутанный клубок ниток: по такой же замысловатой, никогда не повторяющейся траектории движется система в период кризиса. Так ведет себя атмосфера Земли - хотя погода сегодня похожа на вчерашнюю, она всегда чем-то от нее отличается, и нет двух одинаковых дней. Так работают сердце и мозг - на их регулярные ритмы наложен хаотический фон, и его исчезновение ведет к скорой смерти пациента.
Этап кризиса характеризуется крайней неустойчивостью: малейшее движение в сторону от траектории может заставить систему сменить сценарий своего развития. Она может отправиться "на второй круг" своей эволюции, лишь немного отличающийся от предыдущего, а может ценой незначительного усилия перейти на принципиально иную, новую орбиту движения. Ведь, действительно, в клубке ниток рядом всегда есть нити, которые ведут в другом направлении, надо лишь "перескочить" на них - и наша судьба резко изменится.
В математических моделях, как ранее было показано, выйти из кризиса можно за счет изменения так называемых внешних параметров - рано или поздно они изменят среду так, что в ней исчезнет неустойчивость, порождающая хаос, и клубок траекторий вытянется во множество почти параллельных нитей. Резкие изменения сценария развития на таких этапах спокойного развития практически невозможны - ведь все нити идут в одном направлении, и требуется долгое путешествие с нитки на нитку, чтобы существенно поменять направление движения.
Образом преодоления кризиса в мифологических концепциях служит ковчег - корабль, несущий семена новой жизни по бушующему морю во время потопа. Ковчег преодолевает хаос благодаря вере капитана, знающего, что потоп не вечен, имеющего ясную цель и осознающего свою ответственность за будущее. Универсальные математические сценарии развития тоже говорят о преходящем характере хаоса. И чтобы не застрять в бессмысленных метаниях, надо успокоиться, не упустить момент окончания кризиса, уловить нужную тенденцию и без лишних затрат выйти на устойчивую траекторию.
Сейчас предмет изучения науки - мир, для которого характерны постоянные кризисы и обвальные процессы, все чаще встречающиеся в нашей повседневной жизни; мир неустойчивостей, когда малые и локальные изменения влекут за собой глобальные последствия (мы можем легко проследить это в нынешнем глобальном конфликте, проанализировав события начиная с 2014 г.); мир, в котором идут процессы становления и возникновения порядка из хаоса; мир, в котором чередующиеся этапы предопределенности и непредсказуемости образуют причудливую череду событий, которые нас окружают и частью которых мы являемся.
Теория катастроф, наряду с другими современными теориями динамических систем, уже в значительной степени изменила привычные представления об устойчивости и инерционности мира. Благодаря ей понятна степень ответственности власть имущих за возможные нарушения гармонии и равновесия. Если кризис, в очередной раз в истории, произойдёт на глобальном, общемировом уровне, произойдет, то слова творца теории катастроф французского ученого Рене Тома можно считать пророческими для его времени:
"Быть может, удастся доказать неизбежность некоторых катастроф, например войн или смерти. Познание не обязательно будет обещанием успеха или выживания: оно может вести также к уверенности в нашем поражении, в нашем конце".
ЛИТЕРАТУРА
Арнольд В. И. Теория катастроф. М.: МГУ. 1983.
Гилмор Р. Прикладная теория катастроф. М.. «Мир». 1984.
Постон Т., Стюарт Я. Теория катастроф и её приложения. М.. «Мир», 1980.
Томпсон Дж. М. Т. Неустойчивости и катастрофы в науке и технике. М «Мир», 1985