Традиционные графики по выборам мэра Москвы 8 сентября 2013 г.

[kurtinna]

Оригинал взят у eugenyboger в Традиционные графики по выборам мэра Москвы 8 сентября 2013 г.
Последние данные ЦИК по 3595 участкам.

1. Самая интересная картинка: гистограмма распределения процента за Собянина, взвешенная на размер участка (графа 1 в протоколе). Если совсем просто, то для каждого значения процента за Собянина (ось X) по оси Y отложена общее списочное количество избирателей на участках, на которых получился соответствующий результат. Такое взвешивание позволяет корректно учитывать абсолютное влияние возможных фальсификаций, а так же исключить артефакты деления от маленьких чисел.
   Процент здесь и далее посчитан стандартным способом, используя общее количество найденных в урнах бюллетеней.
   
   Фит распределением гаусса.
   
   
   
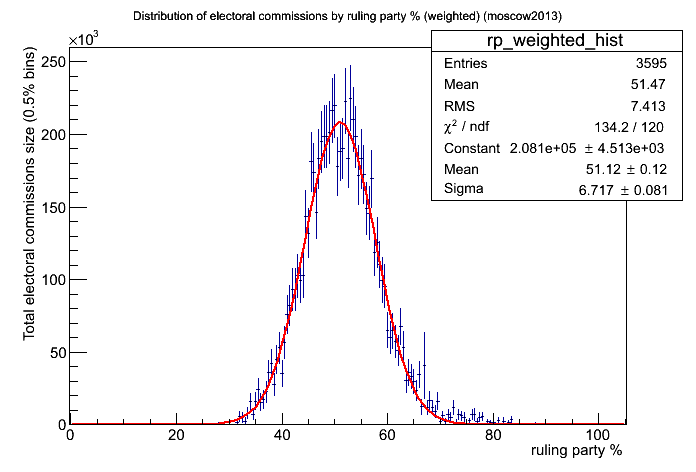
   Выводы: гистограмма процента за Собянина просто прекрасно описывается нормальным распределением. Исключение составляет участок у правого хвоста распределения, где можно заметить превышение уровня над ожидаемым распределением. Т.к. гаусс - распределение симметричное и данные им неплохо описываются, то наиболее вероятное значение процента за Собянина приблизительно соответствует искомому среднему.
   
   Среднее значение модели в правом верхнем углу графика, находится в районе 51.0%. Значение очень незначительно меняется (сотые процента), если выкидывать из рассмотрения данные в районе подозрительного выброса справа (напомню, что это не означает исключения комиссий с большим процентом за Собянина из подсчёта результатов, они лишь не участвуют в построении модели, которая неплохо строится и по остальным данным).
   
   Объём фальсификаций в подсчёте итогов голосования, если они встречались локально, не превышает 0.5% по предварительной оценке.
2. Взвешенное распределение явки, фит гауссом.
   
   
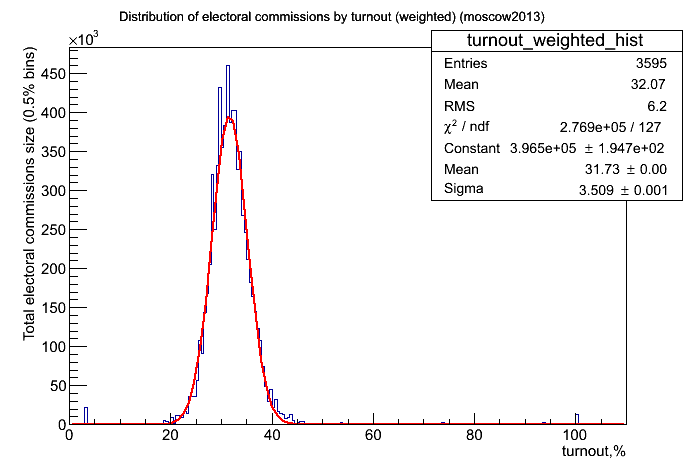
   Почти то же самое: незначительно превышение справа на хвосте.
3. Двумерная взвешенная гисторамма: процент за Собянина от явки.
   
   
   
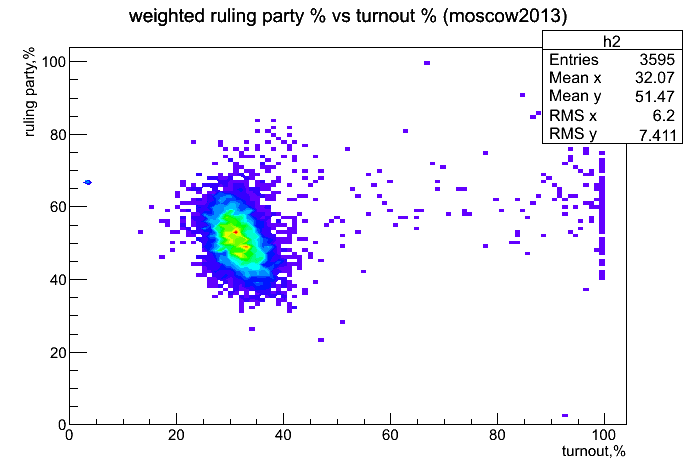
   Выводы: выглядит прилично, видна отрицательная корреляция процента за Собянина и явки. Чем больше приходило людей на участки, тем хуже был результат Собянина . Что подтверждает печальный факт: не все противники действующей власти были мобилизованы на выборы.
   
   UPDATE: как правильно и неоднократно было отмечено в комментариях, сама по себе корреляция не позволяет сделать такие выводы. Данные согласуются с гипотезой, не более.
   
   Коэффициент корреляции в центральном регионе: -0.28.
   
4. Фит слайсов (оно же profile) предыдущей картинки. Простыми словами: для каждого значения явки была построена гистограмма распределения процента голосов за Собянина. По этой гистограмме считается среднее и дисперсия. Среднее значение, получившееся в такого фита, отложено по оси Y.
   
   Красная линия - фит центрального региона прямой. Коэффициенты справа.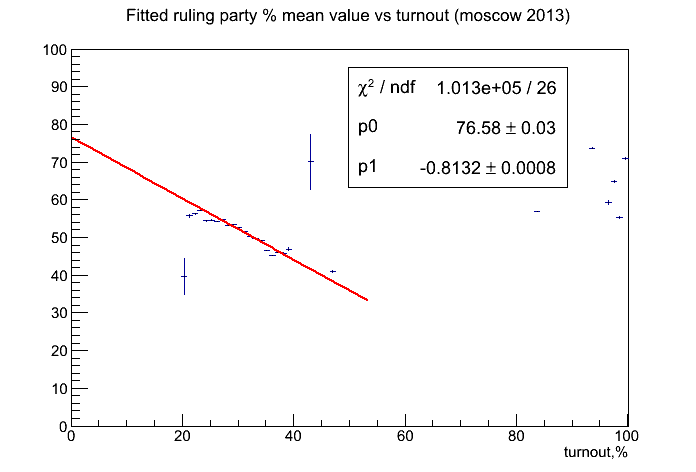
   
   
   Выводы: Угловой коэффициент -0.8 как бы намекает на масштаб эффекта.
   
   UPDATE: важное пояснение:
   
   Это весьма специфичный график, называется profile. Особенность в том, что точка и погрешность там означают всего лишь среднее и дисперсию в соответствующем срезе исходной двумерной гистограммы. Соответственно на срезах, на которых мало данных, достоверность этих точек практически никакая.
   
   Например, если на каком-нибудь срезе была всего лишь одна точка, например в 91%, то на profile будет точка в 91% с нулевым размером креста.
   
   В общем смотреть на profile за пределы центрального пятна на 2d-гистограмме смысла нет.
   Ну и вообще, не стоит путать наклон прямой по центральному гребню и собственно коэффициент корреляции. И явка, и процент за собянина имеют значительную дисперсию. Никаких предсказаний типа, "если на участке такая-то явка, то там такой-то процент" делать конечно же нельзя.
   
   

Все данные, скрипты и картинки в репозитории https://github.com/evgeny-boger/rus-elections-stats/

Важный вывод из всего этого: товарищи эксперты, утверждавшие, что нормальное распределение не применимо для описания выборов вообще, российских выборов, московских выборов и т.д. очевидно окончательно оказались неправы. Именно так должны выглядеть графики для честных результатов голосования, хотя бы в масштабе одного региона. Стоит ли говорить, что на президентских и думских выборах всё выглядело немного не так.