Композиция из 4-х треугольников

Нашёл великолепную задачу, возможно принадлежащую французскому математику Ноэлю.
Вершины трёх равносторонних треугольников с общей вершиной соединены тремя отрезками так, как показано на рисунке. Доказать, что треугольник с вершинами в серединах этих отрезков также равносторонний.
Открыв апплет и подвигав отмеченные точки, можно увидеть всё богатство замечательной конфигурации. Для доказательства, на мой взгляд, проще всего использовать комплексные числа, следующую теорему.
Пусть на комплексной плоскости задан положительно ориентированный треугольник АВС, вершинам которого соответствуют комплексные числа a, b, c. Тогда треугольник АВС правильный в том и только в том случае, если
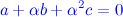
, где
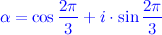
.