Ж Е СС Ь
Математики заявили о доказательстве гипотезы Роты

Жан-Карло Рота
В середине августа 2013 года трое математиков - Джоф Уиттл, Джим Джилин и Бера Гегардз - объявили, что им удалось доказать гипотезу Роты. Эта гипотеза, сформулированная Жан-Карло Ротой в 1970-м году, относится к матроидам - объектам, крайне популярным в комбинаторике и геометрии. Работа математиков еще не опубликована, однако у специалистов, похоже, нет сомнений в том, что гипотеза доказана.
«Мы больше не в Матрице»
Сам термин «матроид» возник в работе «Абстрактные свойства линейной зависимости» (.pdf) Хасслера Уитни в 1935 году. Мы начнем с абстрактного определения этого объекта, а затем покажем, как он естественным образом возникает в самых разных задачах - от геометрии до программирования.
Итак, пусть дано некоторое конечное множество E. Оно называется носителем матроида. Среди всех подмножеств этого множества выделен некоторый набор подмножеств I, удовлетворяющий трем условиям:
1) Набор содержит пустое множество.
2) Если набор содержит подмножество H, то он содержит и все подмножества H.
3) Если H и K - два разных подмножества E, содержащиеся в I, причем в H элементов меньше, чем в K, то в K можно выбрать такой элемент a, что, добавив его к H, мы получим подмножество H', также лежащее в I.
Подмножества, попавшие в набор I, называются независимыми. В свою очередь, не попавшие - зависимыми.
Для того чтобы это абстрактное определение было проще усвоить, приведем несколько примеров. Рассмотрим носитель E, состоящий из одного элемента {x}. Множество всех подмножеств такого носителя состоит ровно из двух подмножеств - пустое подмножество и подмножество, состоящее из {x}. Учитывая, что по первому условию в определении матроида пустое множество должно всегда попадать в набор I, вариантов этого набора остается ровно два - пустое множество и пустое подмножество вместе со всем множеством. Для обоих наборов остальные свойства из определения матроида, очевидным образом, выполняются.
Если в носителе E два элемента {x, y}, то, с учетом пустого подмножества, у такого множества ровно 4 подмножества. Всего можно придумать 15 наборов подмножеств. Матроидов будет много меньше. Действительно, возьмем подмножество с максимальным числом элементов, входящее в матроид. Если в таком множестве 0 элементов, то матроид состоит только из пустого множества; если это число равно 1, то матроидов три - содержащие в довесок к пустому множеству либо {x}, либо {y}, либо оба из этих подмножеств; если же число равно двум, то по третьему пункту в определении такой матроид единственный и содержит все подмножества E. То есть всего мы получили пять матроидов на двуэлементном носителе.
Пусть теперь E состоит из n элементов. Универсальным матроидом Uk, n называется матроид, состоящий из всех подмножеств множества E, в которых не более k элементов. Построенные выше для одноэлементного носителя матроиды являются универсальными и обозначаются U0, 1 и U1, 1. Из пяти матроидов для двухэлементного множества три являются универсальными - это U0, 2, U1, 2 и U2, 2.
Пусть программисту-фрилансеру Васе Пупкину дано n заданий. Для каждого задания известен его дедлайн, а также стоимость (то есть если Вася не выполняет задание, то теряет столько-то денег). Вася настолько крут, что за один день может сделать одно задание. Выполнение задания можно начать с момента 0. Нужно максимизировать прибыль.
Классический пример поведения жадины: Васе выгодно делать самые дорогие задания, а самые дешевые можно и не выполнять - тогда прибыль будет максимальна. Возникает вопрос: каким образом распределить задания? Будем перебирать задания в порядке убывания стоимости. При этом заполнять расписание станем так: если на очередном шаге для заказа есть хотя бы одно свободное место (то есть пустой день в расписании) до наступления дедлайна, то из всех таких «дырок» выберем самую позднюю в смысле даты (но чтобы до дедлайна). В противном случае в срок мы его все равно не можем выполнить, поэтому забиваем на него.
habrahabr.ru
Помимо самого определения матроида нам потребуется понятие минора матроида. Минор - это некоторый новый матроид, получаемый из исходного при помощи двух операций - ограничения и сжатия.
Ограничение работает следующим образом - мы берем и выбрасываем из E некоторое количество элементов. Остается множество, которое мы обозначим S. Если на E был задан матроид M, то оставляем только те независимые подмножества, которые целиком попали в S. Результат такого выбрасывания оказывается матроидом уже на S и называется результатом ограничения матроида на S.
Рассмотрим работу этой операции на примере. Возьмем уже знакомый нам двуэлементный носитель E и выкинем из него один элемент. В результате получим одноэлементный носитель S. Легко проверяется, что при ограничении на S матроид U2, 2 превращается в U1, 1. При этом, ограничение на S U1, 2 также дает U1, 1. В общем, операция не самая простая.
Сжатие матроида устроено несколько сложнее. Из E снова выкидываются некоторые элементы, чтобы осталось множество S. При этом носителем сжатия будут выкинутые элементы. Подмножество H такого носителя называется независимым, если после добавления к нему любого независимого множества из S получается независимое множество в исходном матроиде. Сжатие матроида U2, 2 на одноэлементное подмножество снова дает U1, 1.
Теперь, когда с мотивацией покончено, можно перейти к содержательным с точки зрения теории примерам матроидов. Итак, пусть задана обычная матрица - прямоугольная таблица с m строками и n столбцами. Столбцы матрицы можно складывать (покомпонентно), умножать на число (тоже покомпонентно). Набор столбцов s1, …, sk называется линейно зависимым, если найдутся такие числа ai (среди них должно быть хотя бы одно ненулевое), что, перемножив столбцы на эти числа и сложив, то есть a1s1 + … + aksk, мы получим нулевой столбец.
Рассмотрим несколько примеров. Если k = 1, то столбец должен быть нулевым, так как a1 должно быть ненулевым. Если k = 2, то два столбца зависимы тогда и только тогда, когда они пропорциональны с некоторым коэффициентом. Когда k > 2, то ситуация несколько усложняется. Например, если дана матрица 3 на 3, то ее столбцы зависимы, если все три вектора, соответствующие столбцам, лежат в одной плоскости.
Если набор не является зависимым, то, как нетрудно догадаться, он называется независимым. Оказывается, что независимые наборы образуют самый настоящий матроид, который получил название матричного. Именно такие матроиды и рассматривал Уитни. Ему хотелось уйти от традиционного представления о зависимости и независимости столбцов в матрице (на самом деле - наборов векторов в некотором линейном пространстве), которое требует умножения на число и сложения. Вместо этого он поставил перед собой целью разобраться с комбинаторной структурой таких наборов - в чем и преуспел: определение и простота структуры оказались крайне полезны в математике.
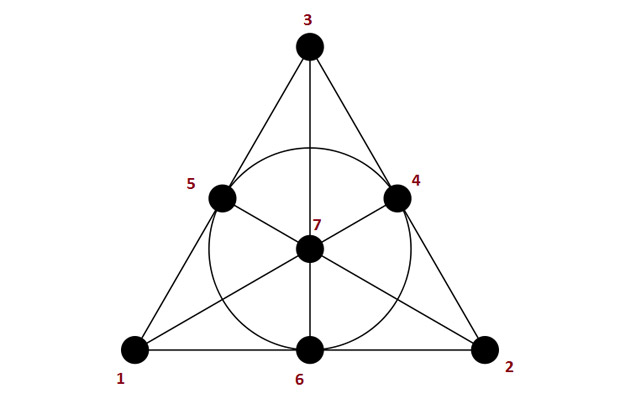
Матроид Фано
Важно понимать, что само понятие матроид - гораздо шире матричного матроида. Уитни удалось обнаружить матроиды, которые нельзя представить в виде матричных. Одним из таких матроидов является матроид Фано (см. картинку). Независимыми считаются наборы из трех точек (и все их подмножества), через которые проходят кривые.
ГРАФОВЫЕ МАТРОЙДЫ
С матричными матроидами тесно связаны графовые матроиды (по сути графовые матроиды могут быть представлены как матричные для некоторой, достаточно большой матрицы, называемой матрицей инцидентности).
Носителем такого матроида выступает множество его вершин. Подмножество вершин, которое образует путь без циклов, называется независимым. Все такие подмножества образуют матроид, который и называется графовым матроидом. Графовый матроид хорош тем, что понятие минора, определяемое в общем случае через ограничение и сжатие, для него значительно упрощается. Минором называется матроид, который построен на графе, полученном из исходного последовательным применением трех операций: удаления ребра; удаление вершины вместе со всеми ребрами, из нее исходящими; склеивание двух вершин, не соединенных ребром.
С графовыми матроидами связано множество замечательных геометрических результатов - сам Уитни доказал множество интересных (правда, довольно технических) теорем, благодаря которым на свет появилась теорема о четырех красках. Самой известной, пожалуй, из теорем такого рода является теорема Вагнера.
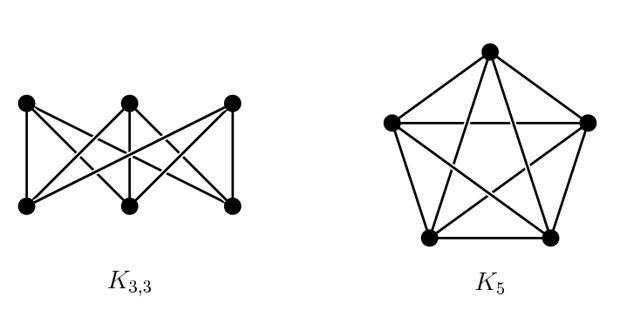
Граф называют плоским, если его можно изобразить на плоскости так, что его ребра не будут пересекаться. Рассмотрим теперь матроиды графов. Будем называть матроид запрещенным минором, если граф, по которому он построен, не плоский, однако, любой его подграф - уже плоский. Легко понять, что граф не плоский, если и только если в качестве одного из своих миноров он содержит запрещенный минор. Теорема Вагнера утверждает, что таких запрещенных миноров всего два. Они соответствуют так называемым графам K5 и K3,3.
В связи с этим известен замечательный факт. Если рисовать графы не на плоскости, а на какой-нибудь другой поверхности, скажем, торе, то матроиды графов K3,3 и K5 не будут запрещенными минорами. Однако, существует результат, что количество таких запрещенных миноров для любой двумерной поверхности будет конечным. Впрочем это количество растет экспоненциально быстро - так, на проективной плоскости 35 запрещенных миноров, в то время как на торе - уже несколько сотен и полный список до сих пор неизвестен.
Zeps"}]">
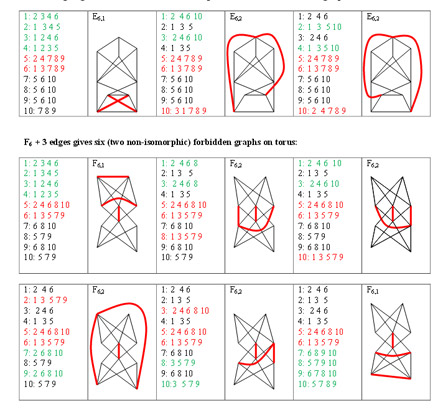
Некоторые запрещенные графы на торе
Zeps
ГИПОТЕЗА РОТЫ
На самом деле идею запрещенных миноров вполне можно обобщить. Действительно, представим, что нас интересует некоторое свойство матроида с условием, что если минор матроида обладает этим свойством, то и весь матроид обязан обладать (в случае с графовыми матроидами это было свойство «граф не является плоским»). Тогда запрещенными минорами будем называть миноры, которые не содержат миноров с нужным нам свойством.
Теперь рассмотрим матроиды и зададимся вопросом, какие из них матричные? Оказывается, свойство матроида не быть матричным как раз подходит для определения запрещенных миноров. В результате, если в матрице стоят действительные числа, то запрещенных миноров бесконечно много (матроид Фано - лишь один из них). Как изменится ситуация, если перейти от поля действительных чисел к конечным полям?
Уильям Татт в 1958 году доказал, что над полем, состоящем из двух элементов Z2 существует ровно один запрещенный минор - это U2, 4. В 1979 году было доказано, что над полем из трех элементов запрещенными являются U2, 5 и U3, 5, а в 2000 году было показано, что над полем из четырех элементов оказалось 7 запрещенных миноров.
В 1978 году Джиан-Карло Рота сформулировал гипотезу: множество запрещенных миноров над каждым конечным полем конечно. Спустя почти 40 лет трое математиков - Джоф Уиттл, Джим Джилин и Бера Гегардз - заявили о доказательстве этой гипотезы. Соответствующий доклад прозвучал еще в июле 2013 года. Пока их работа не опубликована в рецензируемом журнале (да и самой работы пока нет) и ничего не известно про само доказательство. Позволяет ли оно строить запрещенные миноры или хотя бы оценивать их количество? Неизвестно.
Специалисты, однако, сходятся во мнении, что, если кто и мог доказать эту гипотезу, то это Уиттл, Джилин и Гегардз. В общей сложности они потратили на работу над этой гипотезой 15 лет.
ЗЫ;
-- Алгоритм называется жадным, если для поиска оптимального решения задачи на каждом шаге выбирается оптимальное решение. Теорема Радо-Эдмондса утверждает, что жадный алгоритм выдает правильный ответ тогда и только тогда, когда, объект, о котором идет речь, представляет собой матроид. Примерами жадных алгоритмов являются алгоритм Прима, алгоритм Крускала и алгоритм Дейкстры.
-- Графом в математике называется конечное множество точек, некоторые из которых соединены кривыми, называемые ребрами. Путем в графе называется последовательность вершин, где каждая следующая соединена с предыдущей ребром. По сути, это последовательности вершин, которые можно пройти, двигаясь по ребрам графа. Циклом называется путь, который начинается и заканчивается в одной и той же вершине.
-- Полем в математике называется множество с набором операций (обычно их обозначают сложением и умножением), обладающих определенным свойством. Простейший пример поля - это множество действительных чисел. Во-первых, элементы этого множества можно складывать, причем сложение ассоциативно (то есть p + (q + r) = (p + q) + r); коммутативно (от перемены мест слагаемых сумма не меняется); есть нейтральный элемент, называемый нулем (нейтральный, то есть его сумма с любым числом дает это же число), и для каждого элемента q определен обратный -q, сумма с которым дает нейтральный элемент. Во-вторых, элементы этого множества можно умножать, причем умножение также ассоциативно, коммутативно, обладает нейтральным элементом (единица) и для каждого ненулевого q определен обратный элемент 1/q, произведение с которым дает нейтральный элемент, то есть единицу. Сложение и умножение связаны так называемым дистрибутивным законом p (q + r) = pq + pr.

Жан-Карло Рота
В середине августа 2013 года трое математиков - Джоф Уиттл, Джим Джилин и Бера Гегардз - объявили, что им удалось доказать гипотезу Роты. Эта гипотеза, сформулированная Жан-Карло Ротой в 1970-м году, относится к матроидам - объектам, крайне популярным в комбинаторике и геометрии. Работа математиков еще не опубликована, однако у специалистов, похоже, нет сомнений в том, что гипотеза доказана.
«Мы больше не в Матрице»
Сам термин «матроид» возник в работе «Абстрактные свойства линейной зависимости» (.pdf) Хасслера Уитни в 1935 году. Мы начнем с абстрактного определения этого объекта, а затем покажем, как он естественным образом возникает в самых разных задачах - от геометрии до программирования.
Итак, пусть дано некоторое конечное множество E. Оно называется носителем матроида. Среди всех подмножеств этого множества выделен некоторый набор подмножеств I, удовлетворяющий трем условиям:
1) Набор содержит пустое множество.
2) Если набор содержит подмножество H, то он содержит и все подмножества H.
3) Если H и K - два разных подмножества E, содержащиеся в I, причем в H элементов меньше, чем в K, то в K можно выбрать такой элемент a, что, добавив его к H, мы получим подмножество H', также лежащее в I.
Подмножества, попавшие в набор I, называются независимыми. В свою очередь, не попавшие - зависимыми.
Для того чтобы это абстрактное определение было проще усвоить, приведем несколько примеров. Рассмотрим носитель E, состоящий из одного элемента {x}. Множество всех подмножеств такого носителя состоит ровно из двух подмножеств - пустое подмножество и подмножество, состоящее из {x}. Учитывая, что по первому условию в определении матроида пустое множество должно всегда попадать в набор I, вариантов этого набора остается ровно два - пустое множество и пустое подмножество вместе со всем множеством. Для обоих наборов остальные свойства из определения матроида, очевидным образом, выполняются.
Если в носителе E два элемента {x, y}, то, с учетом пустого подмножества, у такого множества ровно 4 подмножества. Всего можно придумать 15 наборов подмножеств. Матроидов будет много меньше. Действительно, возьмем подмножество с максимальным числом элементов, входящее в матроид. Если в таком множестве 0 элементов, то матроид состоит только из пустого множества; если это число равно 1, то матроидов три - содержащие в довесок к пустому множеству либо {x}, либо {y}, либо оба из этих подмножеств; если же число равно двум, то по третьему пункту в определении такой матроид единственный и содержит все подмножества E. То есть всего мы получили пять матроидов на двуэлементном носителе.
Пусть теперь E состоит из n элементов. Универсальным матроидом Uk, n называется матроид, состоящий из всех подмножеств множества E, в которых не более k элементов. Построенные выше для одноэлементного носителя матроиды являются универсальными и обозначаются U0, 1 и U1, 1. Из пяти матроидов для двухэлементного множества три являются универсальными - это U0, 2, U1, 2 и U2, 2.
Пусть программисту-фрилансеру Васе Пупкину дано n заданий. Для каждого задания известен его дедлайн, а также стоимость (то есть если Вася не выполняет задание, то теряет столько-то денег). Вася настолько крут, что за один день может сделать одно задание. Выполнение задания можно начать с момента 0. Нужно максимизировать прибыль.
Классический пример поведения жадины: Васе выгодно делать самые дорогие задания, а самые дешевые можно и не выполнять - тогда прибыль будет максимальна. Возникает вопрос: каким образом распределить задания? Будем перебирать задания в порядке убывания стоимости. При этом заполнять расписание станем так: если на очередном шаге для заказа есть хотя бы одно свободное место (то есть пустой день в расписании) до наступления дедлайна, то из всех таких «дырок» выберем самую позднюю в смысле даты (но чтобы до дедлайна). В противном случае в срок мы его все равно не можем выполнить, поэтому забиваем на него.
habrahabr.ru
Помимо самого определения матроида нам потребуется понятие минора матроида. Минор - это некоторый новый матроид, получаемый из исходного при помощи двух операций - ограничения и сжатия.
Ограничение работает следующим образом - мы берем и выбрасываем из E некоторое количество элементов. Остается множество, которое мы обозначим S. Если на E был задан матроид M, то оставляем только те независимые подмножества, которые целиком попали в S. Результат такого выбрасывания оказывается матроидом уже на S и называется результатом ограничения матроида на S.
Рассмотрим работу этой операции на примере. Возьмем уже знакомый нам двуэлементный носитель E и выкинем из него один элемент. В результате получим одноэлементный носитель S. Легко проверяется, что при ограничении на S матроид U2, 2 превращается в U1, 1. При этом, ограничение на S U1, 2 также дает U1, 1. В общем, операция не самая простая.
Сжатие матроида устроено несколько сложнее. Из E снова выкидываются некоторые элементы, чтобы осталось множество S. При этом носителем сжатия будут выкинутые элементы. Подмножество H такого носителя называется независимым, если после добавления к нему любого независимого множества из S получается независимое множество в исходном матроиде. Сжатие матроида U2, 2 на одноэлементное подмножество снова дает U1, 1.
Теперь, когда с мотивацией покончено, можно перейти к содержательным с точки зрения теории примерам матроидов. Итак, пусть задана обычная матрица - прямоугольная таблица с m строками и n столбцами. Столбцы матрицы можно складывать (покомпонентно), умножать на число (тоже покомпонентно). Набор столбцов s1, …, sk называется линейно зависимым, если найдутся такие числа ai (среди них должно быть хотя бы одно ненулевое), что, перемножив столбцы на эти числа и сложив, то есть a1s1 + … + aksk, мы получим нулевой столбец.
Рассмотрим несколько примеров. Если k = 1, то столбец должен быть нулевым, так как a1 должно быть ненулевым. Если k = 2, то два столбца зависимы тогда и только тогда, когда они пропорциональны с некоторым коэффициентом. Когда k > 2, то ситуация несколько усложняется. Например, если дана матрица 3 на 3, то ее столбцы зависимы, если все три вектора, соответствующие столбцам, лежат в одной плоскости.
Если набор не является зависимым, то, как нетрудно догадаться, он называется независимым. Оказывается, что независимые наборы образуют самый настоящий матроид, который получил название матричного. Именно такие матроиды и рассматривал Уитни. Ему хотелось уйти от традиционного представления о зависимости и независимости столбцов в матрице (на самом деле - наборов векторов в некотором линейном пространстве), которое требует умножения на число и сложения. Вместо этого он поставил перед собой целью разобраться с комбинаторной структурой таких наборов - в чем и преуспел: определение и простота структуры оказались крайне полезны в математике.

Матроид Фано
Важно понимать, что само понятие матроид - гораздо шире матричного матроида. Уитни удалось обнаружить матроиды, которые нельзя представить в виде матричных. Одним из таких матроидов является матроид Фано (см. картинку). Независимыми считаются наборы из трех точек (и все их подмножества), через которые проходят кривые.
ГРАФОВЫЕ МАТРОЙДЫ
С матричными матроидами тесно связаны графовые матроиды (по сути графовые матроиды могут быть представлены как матричные для некоторой, достаточно большой матрицы, называемой матрицей инцидентности).
Носителем такого матроида выступает множество его вершин. Подмножество вершин, которое образует путь без циклов, называется независимым. Все такие подмножества образуют матроид, который и называется графовым матроидом. Графовый матроид хорош тем, что понятие минора, определяемое в общем случае через ограничение и сжатие, для него значительно упрощается. Минором называется матроид, который построен на графе, полученном из исходного последовательным применением трех операций: удаления ребра; удаление вершины вместе со всеми ребрами, из нее исходящими; склеивание двух вершин, не соединенных ребром.
С графовыми матроидами связано множество замечательных геометрических результатов - сам Уитни доказал множество интересных (правда, довольно технических) теорем, благодаря которым на свет появилась теорема о четырех красках. Самой известной, пожалуй, из теорем такого рода является теорема Вагнера.
Граф называют плоским, если его можно изобразить на плоскости так, что его ребра не будут пересекаться. Рассмотрим теперь матроиды графов. Будем называть матроид запрещенным минором, если граф, по которому он построен, не плоский, однако, любой его подграф - уже плоский. Легко понять, что граф не плоский, если и только если в качестве одного из своих миноров он содержит запрещенный минор. Теорема Вагнера утверждает, что таких запрещенных миноров всего два. Они соответствуют так называемым графам K5 и K3,3.

В связи с этим известен замечательный факт. Если рисовать графы не на плоскости, а на какой-нибудь другой поверхности, скажем, торе, то матроиды графов K3,3 и K5 не будут запрещенными минорами. Однако, существует результат, что количество таких запрещенных миноров для любой двумерной поверхности будет конечным. Впрочем это количество растет экспоненциально быстро - так, на проективной плоскости 35 запрещенных миноров, в то время как на торе - уже несколько сотен и полный список до сих пор неизвестен.
Zeps"}]">

Некоторые запрещенные графы на торе
Zeps
ГИПОТЕЗА РОТЫ
На самом деле идею запрещенных миноров вполне можно обобщить. Действительно, представим, что нас интересует некоторое свойство матроида с условием, что если минор матроида обладает этим свойством, то и весь матроид обязан обладать (в случае с графовыми матроидами это было свойство «граф не является плоским»). Тогда запрещенными минорами будем называть миноры, которые не содержат миноров с нужным нам свойством.
Теперь рассмотрим матроиды и зададимся вопросом, какие из них матричные? Оказывается, свойство матроида не быть матричным как раз подходит для определения запрещенных миноров. В результате, если в матрице стоят действительные числа, то запрещенных миноров бесконечно много (матроид Фано - лишь один из них). Как изменится ситуация, если перейти от поля действительных чисел к конечным полям?
Уильям Татт в 1958 году доказал, что над полем, состоящем из двух элементов Z2 существует ровно один запрещенный минор - это U2, 4. В 1979 году было доказано, что над полем из трех элементов запрещенными являются U2, 5 и U3, 5, а в 2000 году было показано, что над полем из четырех элементов оказалось 7 запрещенных миноров.
В 1978 году Джиан-Карло Рота сформулировал гипотезу: множество запрещенных миноров над каждым конечным полем конечно. Спустя почти 40 лет трое математиков - Джоф Уиттл, Джим Джилин и Бера Гегардз - заявили о доказательстве этой гипотезы. Соответствующий доклад прозвучал еще в июле 2013 года. Пока их работа не опубликована в рецензируемом журнале (да и самой работы пока нет) и ничего не известно про само доказательство. Позволяет ли оно строить запрещенные миноры или хотя бы оценивать их количество? Неизвестно.
Специалисты, однако, сходятся во мнении, что, если кто и мог доказать эту гипотезу, то это Уиттл, Джилин и Гегардз. В общей сложности они потратили на работу над этой гипотезой 15 лет.
ЗЫ;
-- Алгоритм называется жадным, если для поиска оптимального решения задачи на каждом шаге выбирается оптимальное решение. Теорема Радо-Эдмондса утверждает, что жадный алгоритм выдает правильный ответ тогда и только тогда, когда, объект, о котором идет речь, представляет собой матроид. Примерами жадных алгоритмов являются алгоритм Прима, алгоритм Крускала и алгоритм Дейкстры.
-- Графом в математике называется конечное множество точек, некоторые из которых соединены кривыми, называемые ребрами. Путем в графе называется последовательность вершин, где каждая следующая соединена с предыдущей ребром. По сути, это последовательности вершин, которые можно пройти, двигаясь по ребрам графа. Циклом называется путь, который начинается и заканчивается в одной и той же вершине.
-- Полем в математике называется множество с набором операций (обычно их обозначают сложением и умножением), обладающих определенным свойством. Простейший пример поля - это множество действительных чисел. Во-первых, элементы этого множества можно складывать, причем сложение ассоциативно (то есть p + (q + r) = (p + q) + r); коммутативно (от перемены мест слагаемых сумма не меняется); есть нейтральный элемент, называемый нулем (нейтральный, то есть его сумма с любым числом дает это же число), и для каждого элемента q определен обратный -q, сумма с которым дает нейтральный элемент. Во-вторых, элементы этого множества можно умножать, причем умножение также ассоциативно, коммутативно, обладает нейтральным элементом (единица) и для каждого ненулевого q определен обратный элемент 1/q, произведение с которым дает нейтральный элемент, то есть единицу. Сложение и умножение связаны так называемым дистрибутивным законом p (q + r) = pq + pr.