Популярное изложение неравенств Белла
В книге “Отличная квантовая механика” я впервые обнаружил некое повествование о неравенствах Белла, не привязанное к физике вообще. Т.е. там приводится аналогия, понятная тем кто не знает физику. Очевидно, для понимания квантовой механики удобно сначала осваивать такие аналогии, а уже потом зубрить матан и прочее. Но у меня создалось ощущение, что в книге что-то напутано.
Процитирую фрагмент книги:
...
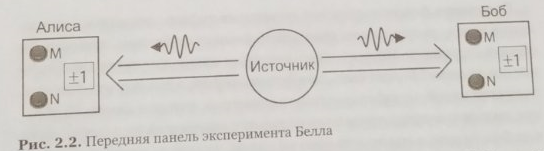
Эта передняя панель выглядит, как показано на рис 2.2. Каждый из двух удалённых наблюдателей - и Алиса, и Боб - пользуются устройством, имеющим две кнопки, обозначенные M и N, и экран, который может показывать либо “+1”, либо “-1”. Во время эксперимента Алиса и Боб не имеют возможности общаться друг с другом.
“Источник”, расположенный примерно посередине между Алисой и Бобом, посылает им пару частиц некоторого рода. Алиса и Боб получают эти частицы и вводят их каждый в своё устройство. Затем они выбирают случайную кнопку на устройстве и одновременно нажимают на неё. Каждое устройство показывает величину +-1, связанную, возможно, с состоянием полученной частицы. Всю описанную операцию мы называем событием.
Оба наблюдателя ведут записи о нажатых ими кнопках и показанных числах. После получения данных о большом массиве событий обе стороны встречаются и производят корреляционный анализ своих событий. А именно, они оценивают величину
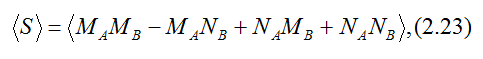
Где
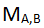
и
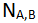
относятся к величинам, полученным каждым наблюдателем при нажатии соответствующей кнопки. Конечно, каждая пара частиц вносит свой вклад только в одно слагаемое в (2.23). Например, если Алиса нажимает M, а Боб - N, то величины, которые они видят при этом на экранах, используются при оценивании
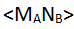
, и т.п.
...
Обратите внимание: утверждение, сделанное выше, неверно, если принцип локальности не работает - например, если
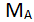
зависит не только от
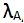
, но также от того, какую кнопку нажал Боб. Эта зависимость сделала бы неверным (2.25), а следовательно, и (2.26).
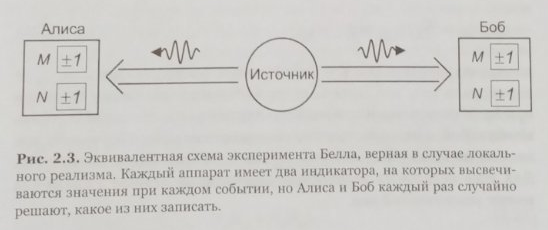
Упражнение 2.47. Выведите неравенство Белла
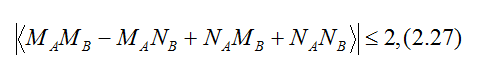
Для любого прибора, передняя панель которого представлена на рис. 2.3.
Подсказка: перепишите (2.26) как
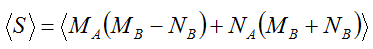
.
Это неравенство применимо и к любому локально-реалистичному устройству с передней панелью Белла (рис. 2.2). И в самом деле, если бы оно не выполнялось для такой установки, оно нарушалось бы также и для её эквивалента на рис 2.3, а мы только что показали, что это невозможно.
..
Конец цитаты.
Судя по всему, в книге идёт речь о неравенствах CHSH:
https://en.wikipedia.org/wiki/CHSH_inequality
Из книги я не понял, как считать S: как сумму усреднённых значений или как усреднённую сумму? В книге вроде написано второе, но по статье из Википедии получается первое. Тут можно сослаться на то, что если проводить эксперимент в соответствии с рисунком 2.3 книги, то это будет одно и то же, поскольку каждый член MaMb, MaNb, NaMb и NaNb ненулевой при каждом событии (генерации пары частиц). Но этот эксперимент соответствует локальному реализму (и S при таком подсчёте никогда не может превысить 2), а нас-то интересует нелокальность, т.е. установка с рис 2.2 книги и эксперимент, где в каждом событии ненулевым является только один член из MaMb, MaNb, NaMb и NaNb.
Если я правильно понимаю суть этой аналогии, то считать S, по-видимому, надо именно как сумму усреднённых значений. Вот пример:
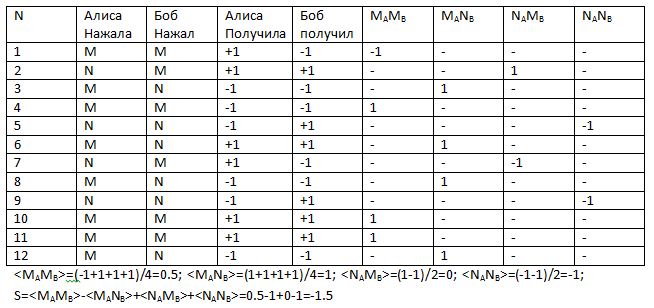
Все мои дальнейшие рассуждения написаны для варианта, что S правильно считается именно так.
Рассуждения у меня получились интересные. Рассмотрим несколько алгоритмов, по которым генерируются измерения Алисы и Боба, и оценим для них S:
1) Кнопка, которую нажимает Алиса, полностью случайная (т.е. она нажимает M или N с равной вероятностью), аналогично для кнопки Боба. Измерение Алисы и Боба также полностью случайные (с равной вероятностью получают +1 или -1). Тогда каждый член суммы MaMb, MaNb, NaMb и NaNb будет с равной вероятностью равен 1 или -1 (это произведение называет корреляцией, т.е. оно равно 1 при полной корреляции измерений и -1 при полной антикорреляции). В среднем эти члены будут давать 0 (чем больше событий, тем ближе к нулю). Значит, S будет равно приблизительно нулю.
2) Кнопки Алисы и Боба полностью случайные, измерение Алисы случайное, а измерение Боба зависит от измерения Алисы, но не зависит от кнопки Алисы. Как я понимаю, зависимость может быть только одна - с какой-то вероятностью совпадение и с оставшейся вероятностью противоположные значения. Например, с вероятностью 80% измерение Боба равно измерению Алисы, а с вероятностью 20% противоположно ему. Тогда каждый член суммы MaMb, MaNb, NaMb и NaNb с вероятностью 80% будет равен 1 и с вероятностью 20% -1. Соответственно при усреднении каждый из этих членов будет равен приблизительно 0.6, а S будет равна приблизительно 1.2. В целом, при корреляции между измерениями Алисы и Боба от -1 до 1, S будет варьировать от -2 до 2.
3) Кнопки случайные, измерение Алисы случайное, а измерение Боба не зависит от измерения Алисы, но зависит от кнопки Алисы. Я не буду останавливаться на этом подробно, но очевидно S будет равно приблизительно 0.
4) Кнопки случайные, измерение Алисы случайное, а измерение Боба зависит как от кнопки Алисы, так и от её измерения. Кратко говоря, с этими алгоритмами S может принимать значения от -4 до 4. Возьмём такой алгоритм: если Алиса нажала M и Боб нажал N, то измерение Боба противоположно измерению Алисы; в противном случае оно совпадает с измерением Алисы. Я буду в дальнейшем называть этот вариант “Алгоритм N 4”. Тогда из компонентов MaMb, MaNb, NaMb и NaNb один - MaNb - будет всегда равен -1, а остальные три будут всегда равны 1; соответственно S всегда будет равно 4. Поскольку |S|>2, мы получили нарушение неравенства Белла, т.е. нелокальность.
Получается, что изложенная простая модель позволяет прочувствовать “философскую суть” квантовой запутанности. С алгоритмом N 4 Алиса не может передать информацию Бобу, нажимая на кнопку неслучайно. Предположим, она всегда будет нажимать M; тогда, если Боб нажмёт M, он получит измерение Алисы (член MaMb), а при нажатии N он получит значение, противоположное измерению Алисы (MaNb). Но измерение Алисы - величина случайная, а произведение случайной на неслучайную величину даёт случайную величину. Т.е. Боб в любом случае будет получать случайный набор цифр и не узнает, что хотела передать Алиса. Это отражает суть квантовой запутанности: она не позволяет передавать информацию, но в то же время не является отсутствием какой-либо связи или взаимодействия. Напомню, что Эйнштейн назвал её “кошмарным дальнодействием”.
Из модели получается вывод, что квантовая запутанность - эта некая “двумерная корреляция”, или “асимметричная корреляция”. В самом деле, измерение Боба не коррелирует с кнопкой Алисы (иначе она могла бы передать Бобу информацию, нажимая на кнопку неслучайно), но в то же время оно каким-то опосредованным способом зависит от её кнопки. И всё это верно в том случае, если алгоритм подсчёта S я понял правильно и вообще данная модель передаёт суть квантовой запутанности.
Если мои рассуждения правильные, следующим шагом я буду изучать, как нарушение неравенств Белла следует из постулатов квантовой механики, начиная с уравнения Максвелла. В книге “Отличная квантовая механика” эта тема рассматривается для поляризации фотонов.
Можно ещё порассуждать по данной модели. Алиса не может передать Бобу информацию, если она сначала нажимает кнопку, а только потом видит своё измерение. Но если бы она сначала увидела измерение, а только потом нажимала кнопку, она могла бы передать информацию Бобу. Предположим, Алиса хочет передать Бобу единицу: тогда она нажимает кнопку, противоположную своему измерению (N для 1 и M для -1). Боб всегда нажимает N. Если, предположим, у Алисы выпало измерение 1, она нажимает N; согласно алгоритму N 4 мы имеем член NaNb, т.е. измерение Боба совпадает с измерением Алисы - Боб получает эту единичку. При измерении -1 у Алисы Боб также получает 1, т.к. срабатывает член MaNb.
Очевидно, в реальных экспериментах такая схема не работает. Мне хотелось бы, чтобы мне это популярно объяснили в терминах не описанного мысленного эксперимента, а реальных спинов электронов или поляризаций фотонов. Вообще, аналогом чего в реальных экспериментах являются кнопка Алисы, кнопка Боба, измерение Алисы, измерение Боба?
Я пока не очень разобрался, является ли алгоритм N 4 симметричным, т.е. зависит ли в нём измерение Алисы от кнопки Боба, подобно тому как измерение Боба зависит от кнопки Алисы. Полагаю, что это так.