Math101 - Lecture 7 revision
The rationals also possess the property called density.
Theorem - Between any two rational numbers a/b < c/d (a, b, c, d ∈ Z) there is an infinite number of rational numbers
Proof: Direct, ‘constructive’ proof.
Note: That (a + mc)/(b + md) always lies between a/b and c/d for m a positive integer (ie m ∈ IN), {(a + mc)/(b + md) : ∈ IN} is an infinite set of rational numbers.
This is easily seen as follows
a/b < (a + mc)/(b + md) if a(b + md) < b(a + mc), but a(b + md) - b(a + mc)
= mad - mbc
= m(md - bc) < 0
As a/b < c/d
∴ a/b < (a + mc)/(b + md)
Similarly (a + mc)/(b + md) < c/d with the same type of proof
-//-
We have “holes” in our number line.
For example, x^2 p/q ∈ Q will not necessarily have a solution, for x in Q - been known since Greek times.
Pythagoras
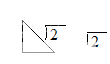
] is not rational.
√2 Is the formal solution of x^2 =2
Theorem √2 is not rational
Proof by contraposition
We assume that x^2 = 2 has a rational solution
x = p/q, p, q integers
We also assume p and q have no common factors.
(If they did we cancelled them)
We have (p/q)^2 = 2 ie p^2 = 2q^2
∴ P^2 is even, hence p is even (p^2 and one p or p must be even!)
Let p = 2m, m an integer As, p^2 = 2q^2, we get 4m^2 = 2q^2
∴ q^2 is even. Hence, q is even. So p and q are both even - they have a common factor of 2.
A contradiction. So √2 is not rational, It is called irrational.
Q together with the irrational numbers give the real numbers, R. The irrational numbers fill in the gaps between the rationals on the real number line,

We can approximate √2 arbitrarily closely using rationals. Decimal approximation from below. 1, 1.4, 1.41, 1.414, 1.4142, ... We get closer and closer to the √2 (never reach it)
These are rational numbers: 1, 14/10, 141/100, 1414/1000
From above.2, 1.5, 1.42, 1415, 1.4143, ...
(They’re all bigger than √2)
We divide a number line into two classes. L - all those to the left of √2 and R all those to the right.