Доказательство гипотезы Коллатца
Гипотеза Коллатца
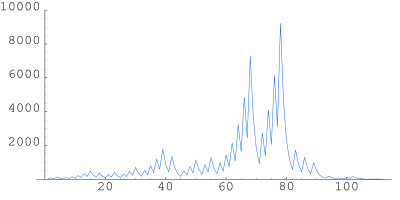

График последовательности для числа 27
Гипо́теза Коллатца (гипо́теза 3n+1, гипо́теза 3x+1, пробле́ма Коллатца, пробле́ма 3n+1, пробле́ма 3x+1, сираку́зская пробле́ма) - одна изнерешённых проблем математики, названная по имени немецкого математика Лотара Коллатца (англ.), предложившего её в 1937 году. Для объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сираку́зской после́довательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее.
Например, для числа 3 получаем:
3 - нечётное, 3×3 + 1 = 10
10 - чётное, 10÷2 = 5
5 - нечётное, 5×3 + 1 = 16
16 - чётное, 16÷2 = 8
8 - чётное, 8÷2 = 4
4 - чётное, 4÷2 = 2
2 - чётное, 2÷2 = 1
1 - нечётное, 1×3 + 1 = 4
Очевидно, что, начиная с 1, начинают циклически повторяться числа 1, 4, 2.
Для числа 27 получаем:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, …
Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232.
Гипотеза Коллатца заключается в том, что какое бы начальное число мы ни взяли, рано или поздно мы получим единицу.
Логическое доказательство гипотезы Коллатца результат с последним числомрезультат с последним числомпромежуточный ррезулльтат (*3)Последующий результат с последним числомколичество делений однозначных чиселколичество делений многозначных чисел21342от 1-n ; и безкон при кратном 2n4390кратен количеству 0 и количеству четных втор значения651562от 1-n ; и безкон при кратном 2n872122от 1-n ; и безкон при кратном 2n092783от 1-n ; и безкон при кратном 2n 3.n где0.(0)1=Вывод: Вариантов деления на (2) у нечетных чисел равно от 1 до бесконечности тогда как вариантов уравнения 3n+1 только 1, при чем "+ 1" рождает нечетное число. В связи с этим если каждое второе действие будет приносить четный результат то количество последовательных делений на 2 в вырастает до 2 раз (50% случаях), следовательно даже при количестве делений (2) сумма числа уменьшается в 4 раза, а уравнение 3n+1
дает максимум увеличение в 3,33333333(3) или в 4 раза если число равно "1". В связи с этим решения приводит к тому, что при постоянном делении на 2 в одно действие увеличивает число в полтора раза +1, что в итоге штудирует числовую прямую на кратные 2 числа, что и приводит к последующему уменьшению числа в много раз в плоть до 1.
Действия деления на 2 в процентах попадания на такое число.
1 действие 100%
2 действия 50%
3 действия 25%
4 действия 12,5%
5 действий 6,25% и т.д.
Приведу таблицу позаимствованную у Эратосфена (решето Эратосфена для нахождения простых чисел)
В таблице выше можно увидеть, что числа по формуле 3*n+1 выпадают каждый 6 раз на числовой прямой начиная с числа 4.
Следующая таблица показывает числа делящиеся на 2 на 4 на 8 на 16 на 32. (1,2,3,4,5 действие)

Анализируя данные факты мы видим, что фактически 50% чисел делятся в 2 и более действий то есть на 4,8,16,32, что в итоге приводит наше значение к 1.
ВСЕ!!!


График последовательности для числа 27
Гипо́теза Коллатца (гипо́теза 3n+1, гипо́теза 3x+1, пробле́ма Коллатца, пробле́ма 3n+1, пробле́ма 3x+1, сираку́зская пробле́ма) - одна изнерешённых проблем математики, названная по имени немецкого математика Лотара Коллатца (англ.), предложившего её в 1937 году. Для объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сираку́зской после́довательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее.
Например, для числа 3 получаем:
3 - нечётное, 3×3 + 1 = 10
10 - чётное, 10÷2 = 5
5 - нечётное, 5×3 + 1 = 16
16 - чётное, 16÷2 = 8
8 - чётное, 8÷2 = 4
4 - чётное, 4÷2 = 2
2 - чётное, 2÷2 = 1
1 - нечётное, 1×3 + 1 = 4
Очевидно, что, начиная с 1, начинают циклически повторяться числа 1, 4, 2.
Для числа 27 получаем:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, …
Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232.
Гипотеза Коллатца заключается в том, что какое бы начальное число мы ни взяли, рано или поздно мы получим единицу.
Логическое доказательство гипотезы Коллатца результат с последним числомрезультат с последним числомпромежуточный ррезулльтат (*3)Последующий результат с последним числомколичество делений однозначных чиселколичество делений многозначных чисел21342от 1-n ; и безкон при кратном 2n4390кратен количеству 0 и количеству четных втор значения651562от 1-n ; и безкон при кратном 2n872122от 1-n ; и безкон при кратном 2n092783от 1-n ; и безкон при кратном 2n 3.n где0.(0)1=Вывод: Вариантов деления на (2) у нечетных чисел равно от 1 до бесконечности тогда как вариантов уравнения 3n+1 только 1, при чем "+ 1" рождает нечетное число. В связи с этим если каждое второе действие будет приносить четный результат то количество последовательных делений на 2 в вырастает до 2 раз (50% случаях), следовательно даже при количестве делений (2) сумма числа уменьшается в 4 раза, а уравнение 3n+1
дает максимум увеличение в 3,33333333(3) или в 4 раза если число равно "1". В связи с этим решения приводит к тому, что при постоянном делении на 2 в одно действие увеличивает число в полтора раза +1, что в итоге штудирует числовую прямую на кратные 2 числа, что и приводит к последующему уменьшению числа в много раз в плоть до 1.
Действия деления на 2 в процентах попадания на такое число.
1 действие 100%
2 действия 50%
3 действия 25%
4 действия 12,5%
5 действий 6,25% и т.д.
Приведу таблицу позаимствованную у Эратосфена (решето Эратосфена для нахождения простых чисел)

В таблице выше можно увидеть, что числа по формуле 3*n+1 выпадают каждый 6 раз на числовой прямой начиная с числа 4.
Следующая таблица показывает числа делящиеся на 2 на 4 на 8 на 16 на 32. (1,2,3,4,5 действие)

Анализируя данные факты мы видим, что фактически 50% чисел делятся в 2 и более действий то есть на 4,8,16,32, что в итоге приводит наше значение к 1.
ВСЕ!!!