Глобализация и стандартизация
Зашел к друзьям-вьетнамцам - смотрят "Кто хочет быть миллионером" - вьетнамскую версию - по пелефону.Но все очень узнаваемо. Глобальная деревня!
А в израильской версии как-то был некорректный вопрос:
В какую игру можно играть на шахматной доске:
А - бридж
В - шашки (по-ивритски - дАмка)
и что-то еще.
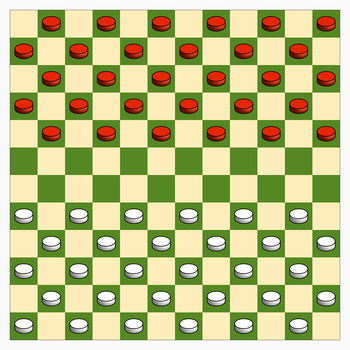
Правильный ответ, конечно, В. Но он - некорректный: можно только в русские шашки, а например, в международные или канадские - нельзя:


Один знакомый #математик, когда его спрашивали, чем он занимается, честно отвечал: "Некорректно поставленными задачами", а когда его спрашивали: "А что это такое?", всегда рассказывал анекдот:
Старик поймал золотую рыбку.
- Старче, загадай своё самое сокровенное желание - и я его исполню.
- Хочу, чтобы моё достоинство было до самой земли.
И ножки его стали укорачиваться, укорачиваться...
Корректные и некорректные задачи, классы математических задач, которые различаются степенью определённости их решений. Многие математические задачи состоят в том, что по исходным данным
u ищется решение z. При этом считается, что u и z связаны функциональной зависимостью z = R (u). Задача называется корректной задачей (или корректно поставленной), если выполнены следующие условия (условия корректности): 1) задача имеет решение при любых допустимых исходных данных (существование решения); 2) каждым исходным данным u соответствует только одно решение (однозначность задачи); 3) решение устойчиво.
Смысл первого условия заключается в том, что среди исходных данных нет противоречащих друг другу условий, что исключало бы возможность решения задачи.
Второе условие означает, что исходных данных достаточно для однозначной определённости решения задачи. Эти два условия обычно называют условиями математической определённости задачи.
Третье условие заключается в следующем. Если u1 и u2 - два различных набора исходных данных, мера уклонения которых друг от друга достаточно мала, то мера уклонения решений z1 = R (u1) и z2 = R (u2)меньше любой наперёд заданной меры точности. При этом предполагается, что в многообразии U = {u} допустимых исходных данных и в многообразии возможных решений Z = {z} установлено понятие меры уклонения (или меры близости) r(u1, u2) и r*(z1, z2). Третье условие обычно трактуется как физическая детерминированность задачи. Это объясняется тем, что исходные данные физической задачи, как правило, задаются с некоторой погрешностью; при нарушении же третьего условия как угодно малые возмущения исходных данных могут вызывать большие отклонения в решении.
Задачи, не удовлетворяющие хотя бы одному условию корректности, называются некорректными задачами (или некорректно поставленными).
Внимание к корректности задач было привлечено французским математиком Ж. Адамаром в связи с решением краевых задач для уравнений с частными производными. Понятие корректности задач явилось, в частности, поводом для классификации краевых задач таких уравнений.
Существовало мнение, что некорректные задачи не могут встречаться при решении физических и технических задач и что для некорректных задач невозможно построение приближённого решения в случае отсутствия устойчивости. Расширение средств автоматизации при получении экспериментальных данных привело к большому увеличению объёма таких данных; необходимость установления по ним информации о естественнонаучных объектах потребовала рассмотрения некорректных задач. Развитие электронной вычислительной техники и применение её к решению математических задач изменило точку зрения на возможность построения приближённых решений некорректно поставленных задач.
А в израильской версии как-то был некорректный вопрос:
В какую игру можно играть на шахматной доске:
А - бридж
В - шашки (по-ивритски - дАмка)
и что-то еще.
Правильный ответ, конечно, В. Но он - некорректный: можно только в русские шашки, а например, в международные или канадские - нельзя:



Один знакомый #математик, когда его спрашивали, чем он занимается, честно отвечал: "Некорректно поставленными задачами", а когда его спрашивали: "А что это такое?", всегда рассказывал анекдот:
Старик поймал золотую рыбку.
- Старче, загадай своё самое сокровенное желание - и я его исполню.
- Хочу, чтобы моё достоинство было до самой земли.
И ножки его стали укорачиваться, укорачиваться...
Корректные и некорректные задачи, классы математических задач, которые различаются степенью определённости их решений. Многие математические задачи состоят в том, что по исходным данным
u ищется решение z. При этом считается, что u и z связаны функциональной зависимостью z = R (u). Задача называется корректной задачей (или корректно поставленной), если выполнены следующие условия (условия корректности): 1) задача имеет решение при любых допустимых исходных данных (существование решения); 2) каждым исходным данным u соответствует только одно решение (однозначность задачи); 3) решение устойчиво.
Смысл первого условия заключается в том, что среди исходных данных нет противоречащих друг другу условий, что исключало бы возможность решения задачи.
Второе условие означает, что исходных данных достаточно для однозначной определённости решения задачи. Эти два условия обычно называют условиями математической определённости задачи.
Третье условие заключается в следующем. Если u1 и u2 - два различных набора исходных данных, мера уклонения которых друг от друга достаточно мала, то мера уклонения решений z1 = R (u1) и z2 = R (u2)меньше любой наперёд заданной меры точности. При этом предполагается, что в многообразии U = {u} допустимых исходных данных и в многообразии возможных решений Z = {z} установлено понятие меры уклонения (или меры близости) r(u1, u2) и r*(z1, z2). Третье условие обычно трактуется как физическая детерминированность задачи. Это объясняется тем, что исходные данные физической задачи, как правило, задаются с некоторой погрешностью; при нарушении же третьего условия как угодно малые возмущения исходных данных могут вызывать большие отклонения в решении.
Задачи, не удовлетворяющие хотя бы одному условию корректности, называются некорректными задачами (или некорректно поставленными).
Внимание к корректности задач было привлечено французским математиком Ж. Адамаром в связи с решением краевых задач для уравнений с частными производными. Понятие корректности задач явилось, в частности, поводом для классификации краевых задач таких уравнений.
Существовало мнение, что некорректные задачи не могут встречаться при решении физических и технических задач и что для некорректных задач невозможно построение приближённого решения в случае отсутствия устойчивости. Расширение средств автоматизации при получении экспериментальных данных привело к большому увеличению объёма таких данных; необходимость установления по ним информации о естественнонаучных объектах потребовала рассмотрения некорректных задач. Развитие электронной вычислительной техники и применение её к решению математических задач изменило точку зрения на возможность построения приближённых решений некорректно поставленных задач.