Орбита. Как определяется орбита.
На волне МЛМ захотелось разобраться с тем, как определяются параметры орбиты. Сам я по роду занятий от космоса далёк, поэтому бекграунда в знаниях - в этой области особо не имею. Про уравнение Кеплера ранее слышал, но не более. Тем более интересно было наконец это всё для себя разъяснить.
Картинок не будет, потому как лениво. Формул тоже, они все есть в википедии.
Ну и в общем то всё это мне интересно в двух аспектах
1. Как описывается орбита,
2. Как "оцифровать" "реальную физичную" орбиту, получившуюся физической симуляцией "в лоб".
Вопрос "получить уравнение эллипса орбиты конкретного тела с конкретными параметрами вне физической симуляции, чисто математически, из масс и энергий" я не ставил, ибо будем реалистами.
Итак. Орбита тела определяется классически шестью параметрами... ну, для позиционирования в простарнстве всегда надо шесть параметров... Орбитой будем считать эллипс. Круг - редкий частный случай, а параболы с гиперболами нам не интересны.
Так вот, "классически", согласно википедии, параметры таковы. Так как их шесть - будем считать список исчерпывающим.
большая полуось [a]
Эксцентриситет орбиты [e]
наклонение [i]
долгота восходящего узла [OMEGA]
аргумент перицентра [omega]
средняя аномалия [M0]
Так вот. Первые два параметра задают вид орбиты. Это "большая полуось", как "длина эллипса", ну или "апогей плюс перигей, считая от центра", и эксцентраситет, который характеризует "сплющенность" эллипса орбиты. Ноль - не сплющен, значит круг, 1 - сплющен "в бесконечность" (то есть незамкнутая парабола). Наш эллипс имеет значение где то между 0 и 1.
Если полёт происходит по физике, то эти два параметра легко получаются из измерений "реальной" орбиты. Апогей и перигей - там понятно, расстояние между этими точками даст большую полуось в виде вектора, измеряем расстояние от оси до перпендикуляра в центре - получаем малую полуось. Три четверти орбиты - и параметры определены. Просимулировать "немного вперёд" - и вот орбита.
Далее, следующие три параметра определяют расположение этого эллипса в пространстве.
Тут требуется "базовая плоскость". В качестве неё, в случае ИСЗ, берётся плоскость экватора. И "базовое направление" в этой плоскости. Например направление на точку весеннего равноденствия. При вращениях Земли - направление "базового направления" не меняется.
Итак. Наклонение орбиты . Угол между плоскостью орбиты и базовой плоскостью. Частный случай - "0" - орбита по экватору. Например геостационар. Или орбита с наклонением оболо 90 градусов - полярная орбита, проходящая над полюсами. Наклонение от 90 до 180 градусов означает обратную орбиту, когда ИСЗ движется не на восток, а на запад.
Угол между плоскостями считается через угол между нормалями. Нормаль экватора у нас есть, это ось вращения Земли. Нормаль орбиты получается из ранее определённых полуосей.
Долгота восходящего узла. Этот параметр определяет, как расположена наклонённая плоскость орбиты вокруг оси вращения Земли.
Математически - это угол в базовой плоскости (то есть в плоскости экватора) между базовым напрпвлением, и направлением на восходящий узел.
Восходящий узел - это точка на орбите, где ИСЗ переходит из южного полушария в северное. То есть прямо на экваторе.
Этот параметр тоже можно получить из измерений "физических координат".
Аргумент перицентра. Этот параметр показывает, грубо говоря, как повёрнут наш эллипс в орбитальной плоскости. Физически - это угол в плоскости орбитальной, между направлением на перицентр и направлением на восходящий узел. Или, иначе говоря, между линией соприкосновения орбитальной и базовой плоскости, и линией, соединяющей апоцентр и перицентр.
И последний, шестой параметр. Аномалия тела. Аномалия тут в значении "особенность".
Этот параметр имеет значение только когда надо показать, в каком месте орбиты должно находиться тело. Если задача "попасть в любое место орбиты" - этот параметр не нужен.
Иными словами - это параметр угла "по орбите".
И вот тут и появляется уравнение Кеплера.
Сложность тут в том, что орбитальная линейная скорость непостоянна. Чем ИСЗ ближе к Земле - тем больше скорость, чем дальше - тем меньше. Угловая скорость из фокуса - вообще меняется весьма замысловата. В Википедии есть весьма понятная анимация. Так вот, закон Кеплера устанавливает связь между равномерным движением воображаемого тела [M], движущегося по воображаемой круговой орбите (с диаметром, равным длине эллипса) (это называют "средняя аномалия"), и такой же воображаемой позицией [E] на той же воображаемой большой круговой орбите. Только если движение [M] равномерное, то движение [E] уже нелинейное. А уж точная позиция ИСЗ на уже эллиптичной орбите - получается опусканием перпендикуляра из точки, куда указывает [E], на большую ось эллипса.
Картинка ниже из Википедии, видно позицию Земли [s], Спутника [p], большую ось эллипса [z] (оно же - направление на перицентр), средняя аномалия[M] указывает на воображаемую точку [y], эксцентрическая аномалия (получаемая через уравнение Кеплера) указывает на точку [x], на перпендикуляре из которой находится наш спутник.
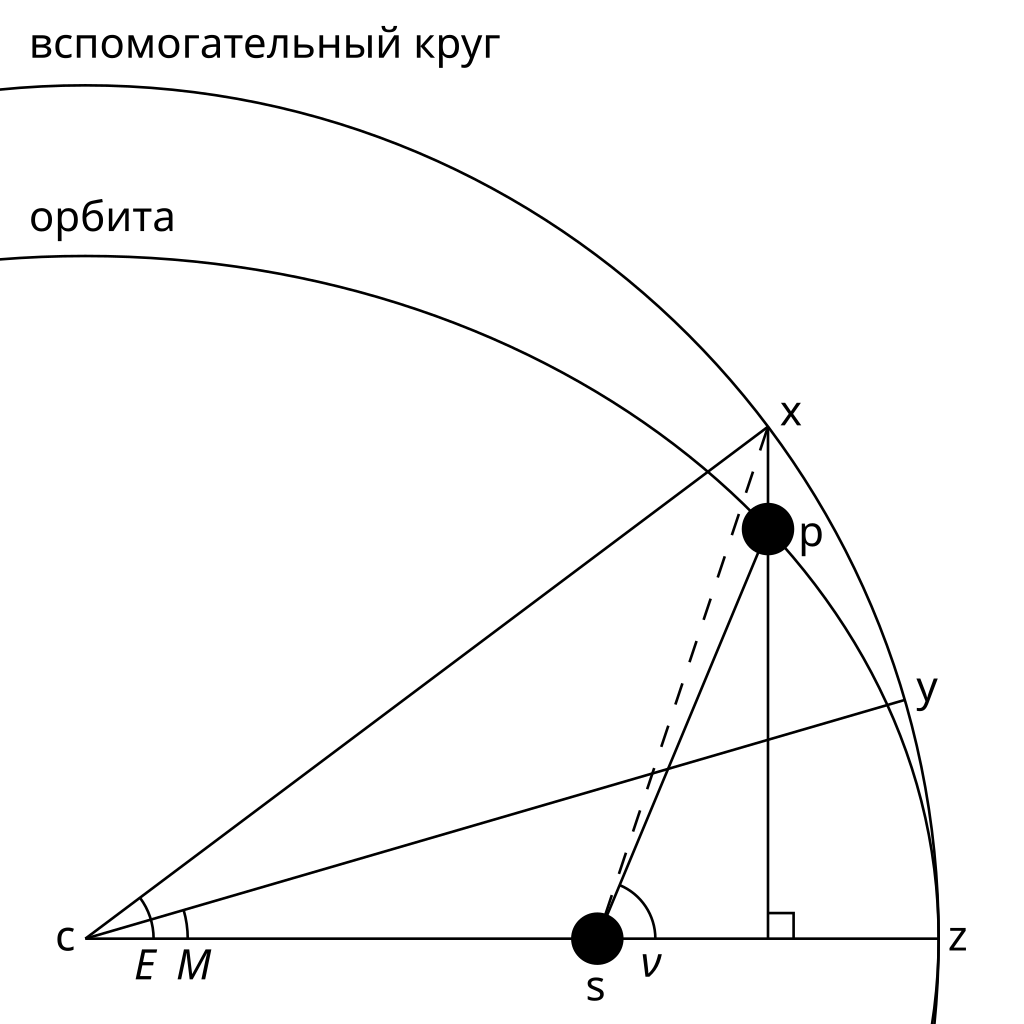
Так вот. Вот эта самая M, как линейно зависящая от времени, и задаёт позицию спутника (ИСЗ) в любой произвольный момент времени начиная с точки отсчёта. А точка отсчёта, с временем [t0], имеет какой то [M0]. Ну то есть сдвиг по орбите, по сути.