Nuclear revision
After seeing the hexagonal Black Box on MathPuzzle.com, I decided to push my hexagonal Magnets-like puzzle, called Nucleus. The groups of three circles are either protons or neutrons, the gray circles are gluons, and the uncolored circles are quarks. Quarks are either red, green, or blue, and though in neutrons they cannot be distinguished, same-colored quarks never touch among protons. Of course, each proton consists of one red, one green, and one blue quark. Given the numbers of distinguishable quarks in some lines, determine the placements of all the protons.
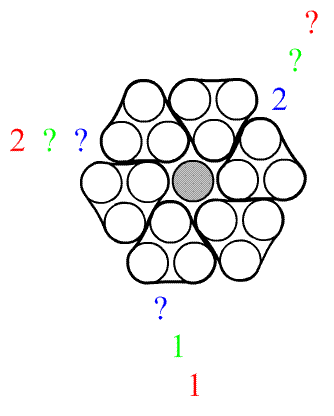
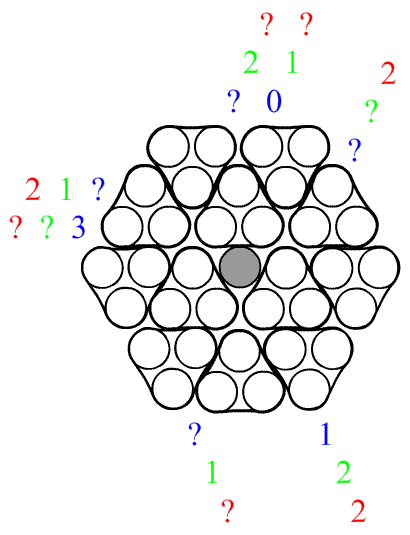
(Oh for crying out loud, why doesn't the spell-check recognize the plural of "gluon"?)
(Edit, 8-14-08: Previous big puzzle wasn't solvable, so I changed it some.)


(Oh for crying out loud, why doesn't the spell-check recognize the plural of "gluon"?)
(Edit, 8-14-08: Previous big puzzle wasn't solvable, so I changed it some.)