Merge Sort на Scala
Сортировка слиянием - один из простейших алгоритмов для упорядочивания списков. Простейший в том смысле, что описание и принцип работы алгоритма легко понять. Средняя скорость работы алгоритма )
, такая же, как у «быстрой сортировки». Однако его реализация на языке Scala обнаруживает некоторые проблемы.
Моя первая реализация выглядела так:
def sort(in: Seq[Int]): Seq[Int] = {
def merge(left: Seq[Int], right: Seq[Int]): Seq[Int] = {
if (left.isEmpty) right
else if (right.isEmpty) left
else if (left.head <= right.head) left.head +: merge(left.tail, right)
else right.head +: merge(left, right.tail)
}
if (in.size <= 1) in
else {
val (left, right) = in.splitAt(in.size / 2)
merge(sort(left), sort(right))
}
}
Это практически дословный перевод описания алгоритма с человеческого на компьютерный. Если на вход подали пустую последовательность или последовательность с одним элементом, то считаем такую последовательность отсортированной. В противном случае делим последовательность пополам, сортируем каждую подпоследовательность и объединяем результаты сортировок.
Самая большая проблема этой реализации - она не может сортировать большие последовательности чисел. Т.е. фактически она непригодна для тех задач, для которых ее изобрели. Например, если на вход подать последовательность из 5000 чисел, произойдет переполнение стека. В таком виде компилятор scala не может преобразовать рекурсивные вызовы merge в хвостовую рекурсию.
Недочет поменьше - нельзя изменить порядок сортировки, не переписывая функцию merge.
Исправленная версия:
def sort(in: Seq[Int], compare: (Int, Int) => Boolean): Seq[Int] = {
@tailrec
def merge(left: Seq[Int], right: Seq[Int], acc: Seq[Int]): Seq[Int] = {
if (left.isEmpty) acc ++ right
else if (right.isEmpty) acc ++ left
else if (compare(left.head, right.head)) merge(left.tail, right, acc :+ left.head)
else merge(left, right.tail, acc :+ right.head)
}
if (in.size <= 1) in
else {
val halfSize = in.size / 2
val (left, right) = in.splitAt(halfSize)
merge(sort(left, compare), sort(right, compare), Seq.empty[Int])
}
}
Теперь функция слияния получает на вход дополнительный параметр - аккумулятор. Такой код будет оптимизирован компилятором. Чтобы отсортировать некоторую последовательность достаточно сделать вызов:
sort(Seq(1, 5, 9, 2, 0), (a, b) => a < b) // будет 0, 1, 2, 5, 9
Но и у этого кода есть проблемы. Он очень и очень медленно работает. Скажем, последовательность из 100 000 случайных чисел он сортирует несколько минут на моем компьютере.
Для сравнения я переписал функцию merge чтобы она не использовала рекурсию и операции с аккумулятором:
def sort(in: Seq[Int], sorted: (Int, Int) => Boolean): Seq[Int] = {
def merge(left: Seq[Int], right: Seq[Int]): Seq[Int] = {
if (right.isEmpty) left
else if (left.isEmpty) right
else {
val result = new Array[Int](left.size + right.size)
var leftIndex = 0
var rightIndex = 0
var resultIndex = 0
while (leftIndex < left.size && rightIndex < right.size) {
if (sorted(left(leftIndex), right(rightIndex))) {
result(resultIndex) = left(leftIndex)
leftIndex += 1
resultIndex += 1
} else {
result(resultIndex) = right(rightIndex)
rightIndex += 1
resultIndex += 1
}
}
while (leftIndex < left.size) {
result(resultIndex) = left(leftIndex)
leftIndex += 1
resultIndex += 1
}
while (rightIndex < right.size) {
result(resultIndex) = right(rightIndex)
rightIndex += 1
resultIndex += 1
}
result
}
}
if (in.size <= 1) in
else {
val halfSize = in.size / 2
merge(sort(in take halfSize, sorted), sort(in drop halfSize, sorted))
}
}
Код читается хуже, содержит в себе var, но работает молниеносно. Почему же производительность предыдущей реализации заметно ниже?
Ответ заключен в этой строчке:
merge(sort(in take halfSize, sorted), sort(in drop halfSize, sorted), Seq.empty[Int])
Компилятор решает заменить Seq.empty[Int] на List.empty[Int]. Согласно таблице характеристик производительности различных видов коллекций в Scala, у List время работы некоторых операций пропорционально длине листа. Функция merge опирается на эти операции, поэтому время работы алгоритма ухудшается до
(грубая оценка). Из всех коллекций только у Vector подходящие характеристики, поэтому я заменил Seq.empty[Int] на него.
Конечный вариант:
def sort(in: Seq[Int], sorted: (Int, Int) => Boolean): Seq[Int] = {
@tailrec
def merge(left: Seq[Int], right: Seq[Int], acc: Seq[Int]): Seq[Int] = {
if (left.isEmpty) acc ++ right
else if (right.isEmpty) acc ++ left
else if (sorted(left.head, right.head)) merge(left.tail, right, acc :+ left.head)
else merge(left, right.tail, acc :+ right.head)
}
if (in.size <= 1) in
else {
val halfSize = in.size / 2
merge(sort(in take halfSize, sorted), sort(in drop halfSize, sorted), Vector.empty[Int])
}
}
Если сравнивать вариант с Vector и вариант без рекурсии в merge, то получается следующая картина:
Vector:
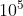
случайных чисел: 1081 мс (лучее из трех измерений)

случайных чисел: 11 с 838 мс (лучее из трех измерений)
merge без рекурсии:
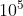
случайных чисел: 381 мс (лучее из трех измерений)

случайных чисел: 2 с 494 мс (лучее из трех измерений)
Код рекурсивной реализации читается легче, но выполняется заметно дольше. В конечном счете, стоит ли оно того? «Некрасивая» реализация выглядит вполне приличной, если бы это был язык Java. Однако в Scala подобный код стараются не писать, всячески избегают «изменения состояния», и неявно создавают при этом медленные программы.
, такая же, как у «быстрой сортировки». Однако его реализация на языке Scala обнаруживает некоторые проблемы.
Моя первая реализация выглядела так:
def sort(in: Seq[Int]): Seq[Int] = {
def merge(left: Seq[Int], right: Seq[Int]): Seq[Int] = {
if (left.isEmpty) right
else if (right.isEmpty) left
else if (left.head <= right.head) left.head +: merge(left.tail, right)
else right.head +: merge(left, right.tail)
}
if (in.size <= 1) in
else {
val (left, right) = in.splitAt(in.size / 2)
merge(sort(left), sort(right))
}
}
Это практически дословный перевод описания алгоритма с человеческого на компьютерный. Если на вход подали пустую последовательность или последовательность с одним элементом, то считаем такую последовательность отсортированной. В противном случае делим последовательность пополам, сортируем каждую подпоследовательность и объединяем результаты сортировок.
Самая большая проблема этой реализации - она не может сортировать большие последовательности чисел. Т.е. фактически она непригодна для тех задач, для которых ее изобрели. Например, если на вход подать последовательность из 5000 чисел, произойдет переполнение стека. В таком виде компилятор scala не может преобразовать рекурсивные вызовы merge в хвостовую рекурсию.
Недочет поменьше - нельзя изменить порядок сортировки, не переписывая функцию merge.
Исправленная версия:
def sort(in: Seq[Int], compare: (Int, Int) => Boolean): Seq[Int] = {
@tailrec
def merge(left: Seq[Int], right: Seq[Int], acc: Seq[Int]): Seq[Int] = {
if (left.isEmpty) acc ++ right
else if (right.isEmpty) acc ++ left
else if (compare(left.head, right.head)) merge(left.tail, right, acc :+ left.head)
else merge(left, right.tail, acc :+ right.head)
}
if (in.size <= 1) in
else {
val halfSize = in.size / 2
val (left, right) = in.splitAt(halfSize)
merge(sort(left, compare), sort(right, compare), Seq.empty[Int])
}
}
Теперь функция слияния получает на вход дополнительный параметр - аккумулятор. Такой код будет оптимизирован компилятором. Чтобы отсортировать некоторую последовательность достаточно сделать вызов:
sort(Seq(1, 5, 9, 2, 0), (a, b) => a < b) // будет 0, 1, 2, 5, 9
Но и у этого кода есть проблемы. Он очень и очень медленно работает. Скажем, последовательность из 100 000 случайных чисел он сортирует несколько минут на моем компьютере.
Для сравнения я переписал функцию merge чтобы она не использовала рекурсию и операции с аккумулятором:
def sort(in: Seq[Int], sorted: (Int, Int) => Boolean): Seq[Int] = {
def merge(left: Seq[Int], right: Seq[Int]): Seq[Int] = {
if (right.isEmpty) left
else if (left.isEmpty) right
else {
val result = new Array[Int](left.size + right.size)
var leftIndex = 0
var rightIndex = 0
var resultIndex = 0
while (leftIndex < left.size && rightIndex < right.size) {
if (sorted(left(leftIndex), right(rightIndex))) {
result(resultIndex) = left(leftIndex)
leftIndex += 1
resultIndex += 1
} else {
result(resultIndex) = right(rightIndex)
rightIndex += 1
resultIndex += 1
}
}
while (leftIndex < left.size) {
result(resultIndex) = left(leftIndex)
leftIndex += 1
resultIndex += 1
}
while (rightIndex < right.size) {
result(resultIndex) = right(rightIndex)
rightIndex += 1
resultIndex += 1
}
result
}
}
if (in.size <= 1) in
else {
val halfSize = in.size / 2
merge(sort(in take halfSize, sorted), sort(in drop halfSize, sorted))
}
}
Код читается хуже, содержит в себе var, но работает молниеносно. Почему же производительность предыдущей реализации заметно ниже?
Ответ заключен в этой строчке:
merge(sort(in take halfSize, sorted), sort(in drop halfSize, sorted), Seq.empty[Int])
Компилятор решает заменить Seq.empty[Int] на List.empty[Int]. Согласно таблице характеристик производительности различных видов коллекций в Scala, у List время работы некоторых операций пропорционально длине листа. Функция merge опирается на эти операции, поэтому время работы алгоритма ухудшается до
(грубая оценка). Из всех коллекций только у Vector подходящие характеристики, поэтому я заменил Seq.empty[Int] на него.
Конечный вариант:
def sort(in: Seq[Int], sorted: (Int, Int) => Boolean): Seq[Int] = {
@tailrec
def merge(left: Seq[Int], right: Seq[Int], acc: Seq[Int]): Seq[Int] = {
if (left.isEmpty) acc ++ right
else if (right.isEmpty) acc ++ left
else if (sorted(left.head, right.head)) merge(left.tail, right, acc :+ left.head)
else merge(left, right.tail, acc :+ right.head)
}
if (in.size <= 1) in
else {
val halfSize = in.size / 2
merge(sort(in take halfSize, sorted), sort(in drop halfSize, sorted), Vector.empty[Int])
}
}
Если сравнивать вариант с Vector и вариант без рекурсии в merge, то получается следующая картина:
Vector:
случайных чисел: 1081 мс (лучее из трех измерений)
случайных чисел: 11 с 838 мс (лучее из трех измерений)
merge без рекурсии:
случайных чисел: 381 мс (лучее из трех измерений)
случайных чисел: 2 с 494 мс (лучее из трех измерений)
Код рекурсивной реализации читается легче, но выполняется заметно дольше. В конечном счете, стоит ли оно того? «Некрасивая» реализация выглядит вполне приличной, если бы это был язык Java. Однако в Scala подобный код стараются не писать, всячески избегают «изменения состояния», и неявно создавают при этом медленные программы.