СВОЙСТВА ДЕВЯТКИ
Некоторые особенности арифметических операций над целыми числами связаны с числом 9. Каждое подмеченное вами свойство девятки может послужить поводом к придумыванию разнообразных математических развлечений. Известен, например, признак делимости на 9: число делится на 9, если сумма его цифр делится на девять. Отсюда следует, что сумма цифр в произведении любого числа на 9 равна девяти или кратна девяти (то-есть делится на девять). Например, 354*9 = 3186, тогда 3+1+8+6 = 18 (делится на девять).
Поэтому, когда один малыш жаловался, что ему трудно запомнить таблицу умножения первых десяти чисел на девять, то отец малыша предложил ему простой способ помочь памяти пальцами своих рук.
Вот этот способ в пользу и помощь другим.
Движением пальца. Положите обе руки рядом на стол и протяните пальцы. Каждый палец слева направо будет означать соответствующее порядковое число: первый слева - 1, второй-2, третий-3, четвертый-4 и т. д. до десятого, который будет обозначать число 10. Пусть требуется умножить теперь любое число из первого десятка на 9. Для этого вам стоит только, не сдвигая рук со стола, приподнять вверх тот палец, который обозначает множимое. Тогда число остальных пальцев, лежащих налево от поднятого пальца, будет числом десятков произведения, а число пальцев направо - числом единиц.
Пример. Умножить 7 на 9. Кладите руки на стол и поднимите седьмой палец (рис. 1); налево от поднятого пальца лежат 6 пальцев, а направо - 3. Значит, результат умножения 7 на 9 равен 63.
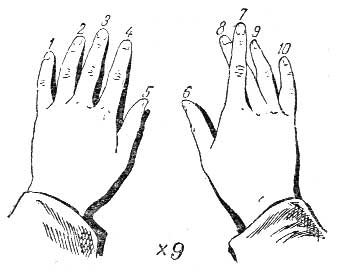
Рис. 1. «Счетная машина».
Это удивительное на первый взгляд механическое умножение тотчас же станет понятным, если вспомнить, что сумма цифр в каждом произведении чисел таблицы умножения на девять равна девяти, а число десятков в произведении всегда на 1 меньше того числа, которое мы умножаем на 9. Поднятием соответствующего пальца это мы и отмечаем, а следовательно, и... умножаем.
Человеческая рука есть одна из первых счетных машин!
Еще некоторые свойства. Вот еще несколько интересных и полезных для дальнейшего свойств, связанных с числом 9.
1. Всегда делится на 9:
а) разность между любым числом и сумной его цифр;
б) разность двух чисел с одинаковыми цифрами, но разным порядком их расположения;
в) разность двух чисел с одинаковыми суммами цифр у каждого из них.
2. Если из каких-либо цифр составлены числа, отличающиеся только порядком следования цифр, то при де-. лении на 9 каждого из них получается один и тот же остаток. Он равен остатку от деления на 9 суммы цифр какого-либо из упомянутых чисел.
3. Если остаток от деления суммы цифр числа на. 9 будем называть «излишком», то:
а) излишек суммы/разность чисел равен излишку суммы/разность излишков слагаемых;
б) излишек произведения двух чисел равен излишку произведения излишков данных чисел.
Вы легко проверите эти свойства на числовых примерах, а если знакомы с алгеброй, то можете их доказать.
В качестве самостоятельного упражнения найдите аналогичное соотношение для излишка частного от деления двух чисел.
Разобравшись в решении задач этой главы, вы можете многие из них использовать в качестве математических фокусов.
Какая цифра зачеркнута?
Задача 1. Пусть ваш друг напишет, не показывая вам, число из трех или более цифр, разделит его на 9 и назовет вам остаток от такого деления. Теперь предложите ему зачеркнуть во взятом им числе одну цифру (любую); число, образовавшееся после зачеркивания цифры, пусть он опять разделит на 9 и снова назовет вам остаток от этого деления. Тотчас же вы можете сказать, какая цифра была зачеркнута, руководствуясь следующими правилами:
а) если второй остаток меньше первого, то, вычитая из первого остатка второй, вы получите как раз зачеркнутую цифру;
б) если второй остаток больше первого, то зачеркнутую цифру вы получите, вычитая второй остаток из первого, увеличенного на 9;
в) если остатки равны, то зачеркнута либо цифра 9, либо 0. Почему так?
doshkolnik.ru
Поэтому, когда один малыш жаловался, что ему трудно запомнить таблицу умножения первых десяти чисел на девять, то отец малыша предложил ему простой способ помочь памяти пальцами своих рук.
Вот этот способ в пользу и помощь другим.
Движением пальца. Положите обе руки рядом на стол и протяните пальцы. Каждый палец слева направо будет означать соответствующее порядковое число: первый слева - 1, второй-2, третий-3, четвертый-4 и т. д. до десятого, который будет обозначать число 10. Пусть требуется умножить теперь любое число из первого десятка на 9. Для этого вам стоит только, не сдвигая рук со стола, приподнять вверх тот палец, который обозначает множимое. Тогда число остальных пальцев, лежащих налево от поднятого пальца, будет числом десятков произведения, а число пальцев направо - числом единиц.
Пример. Умножить 7 на 9. Кладите руки на стол и поднимите седьмой палец (рис. 1); налево от поднятого пальца лежат 6 пальцев, а направо - 3. Значит, результат умножения 7 на 9 равен 63.

Рис. 1. «Счетная машина».
Это удивительное на первый взгляд механическое умножение тотчас же станет понятным, если вспомнить, что сумма цифр в каждом произведении чисел таблицы умножения на девять равна девяти, а число десятков в произведении всегда на 1 меньше того числа, которое мы умножаем на 9. Поднятием соответствующего пальца это мы и отмечаем, а следовательно, и... умножаем.
Человеческая рука есть одна из первых счетных машин!
Еще некоторые свойства. Вот еще несколько интересных и полезных для дальнейшего свойств, связанных с числом 9.
1. Всегда делится на 9:
а) разность между любым числом и сумной его цифр;
б) разность двух чисел с одинаковыми цифрами, но разным порядком их расположения;
в) разность двух чисел с одинаковыми суммами цифр у каждого из них.
2. Если из каких-либо цифр составлены числа, отличающиеся только порядком следования цифр, то при де-. лении на 9 каждого из них получается один и тот же остаток. Он равен остатку от деления на 9 суммы цифр какого-либо из упомянутых чисел.
3. Если остаток от деления суммы цифр числа на. 9 будем называть «излишком», то:
а) излишек суммы/разность чисел равен излишку суммы/разность излишков слагаемых;
б) излишек произведения двух чисел равен излишку произведения излишков данных чисел.
Вы легко проверите эти свойства на числовых примерах, а если знакомы с алгеброй, то можете их доказать.
В качестве самостоятельного упражнения найдите аналогичное соотношение для излишка частного от деления двух чисел.
Разобравшись в решении задач этой главы, вы можете многие из них использовать в качестве математических фокусов.
Какая цифра зачеркнута?
Задача 1. Пусть ваш друг напишет, не показывая вам, число из трех или более цифр, разделит его на 9 и назовет вам остаток от такого деления. Теперь предложите ему зачеркнуть во взятом им числе одну цифру (любую); число, образовавшееся после зачеркивания цифры, пусть он опять разделит на 9 и снова назовет вам остаток от этого деления. Тотчас же вы можете сказать, какая цифра была зачеркнута, руководствуясь следующими правилами:
а) если второй остаток меньше первого, то, вычитая из первого остатка второй, вы получите как раз зачеркнутую цифру;
б) если второй остаток больше первого, то зачеркнутую цифру вы получите, вычитая второй остаток из первого, увеличенного на 9;
в) если остатки равны, то зачеркнута либо цифра 9, либо 0. Почему так?
doshkolnik.ru