Epidemic outbreak mathematical model (free article)
Simple mathematical model of epidemic outbreak (free article)
Amateur translation
First St. Petersburg State Medical University named after I.P. Pavlov
https://studfile.net/preview/5845326/page:13/
Over the past many years of human existence, a huge number of people have died from various epidemics. Plague, cholera, flu, etc. often affected a significant mass of people. In order to be able to deal with epidemics, i.e. timely use of certain medical measures (quarantines, vaccinations, etc.), it is necessary to be able to compare the effectiveness of these measures. They can only be compared if it is possible to predict how the course of the epidemic will change during a given event, i.e. how the number of cases will change.
Hence, the need arises to build a model that could serve the purpose of the forecast.
For simplicity, we consider the natural course of the epidemic without any intervention and try to predict the consequences.
Since our goal is only to create an illustrative model, here we abstract from very many factors (conditions for the reproduction of bacterial cells, the degree of susceptibility to infection of individuals, the probability of meeting the carrier of infection with a healthy person, etc.)
So, let there be N healthy people, and at time t = 0 one sick person falls into this group - the source of infection. We will assume that no removal of patients from the group occurs. We also believe that a person becomes a source of infection immediately after he becomes infected.
Suppose at some point in time t
X (t) is the number of sources of infection,
Y (t) - the number of people who can get sick,
Then we have X (t) + Y (t) = N + 1 at any time.
For t = 0, the condition X (0) = 1
The number of new dX patients that appeared over the period of time dt will be proportional to the number of meetings of healthy and sick people, i.e. product of XY quantities. Therefore, you can write
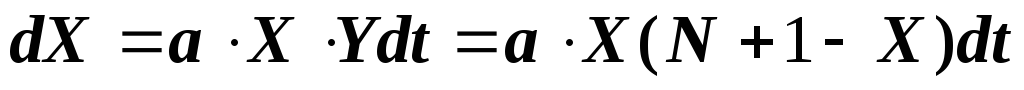
or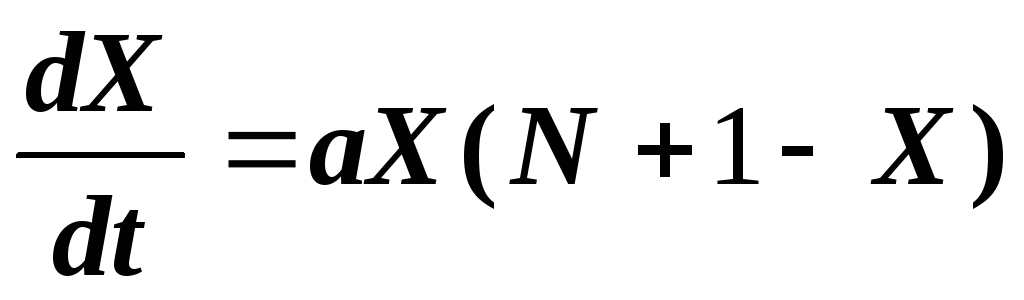
where a is the coefficient of proportionality.
The resulting differential equation together with the condition X (0) = 1 determines the function X (t), i.e. the number of cases at time t.
We find a general solution, after separating the variables.
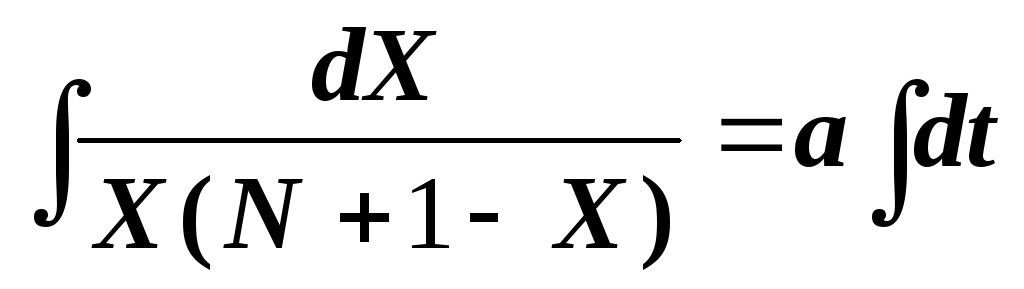
To take the first integral, divide the numerator and denominator of the fraction by
and introduce a new variable
, then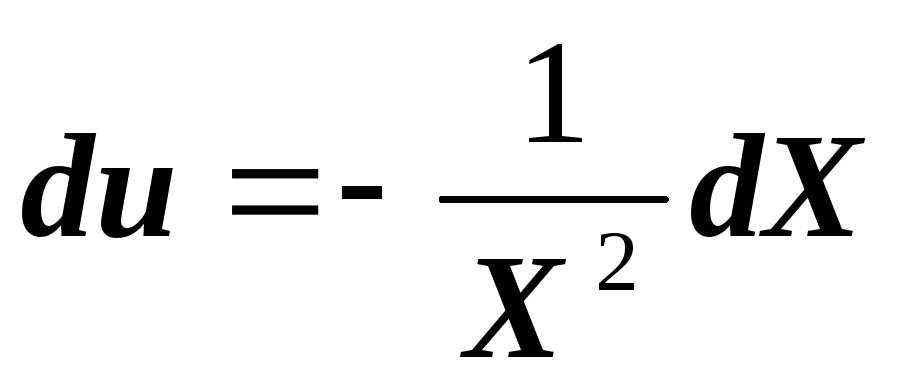
,.and from here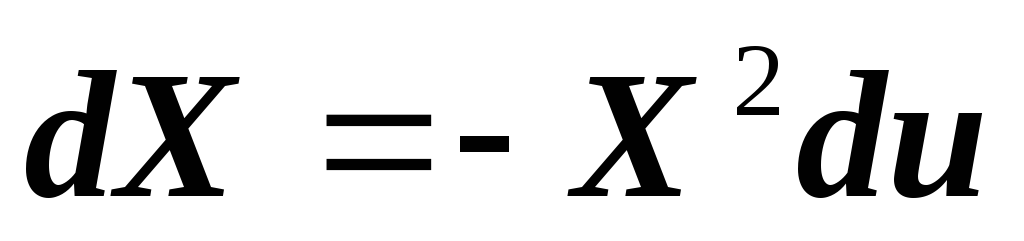
.
We replace the variable under the integral, and we obtain

After integration, we have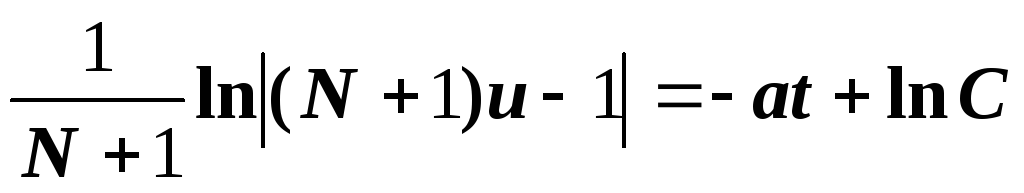
and therefore
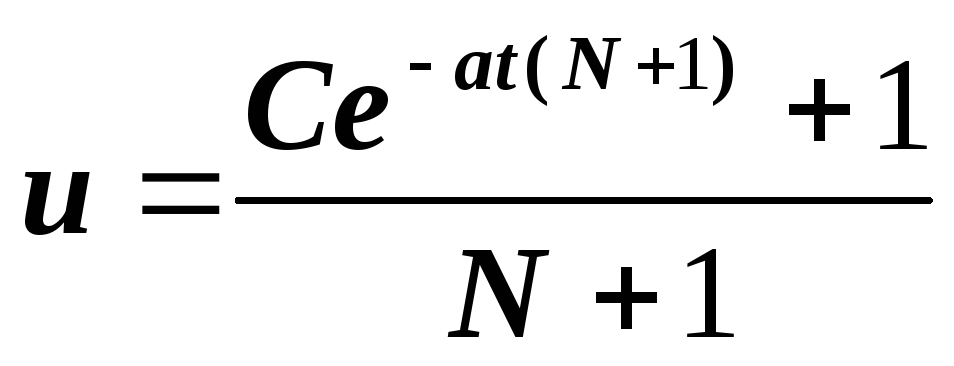
Given the fact that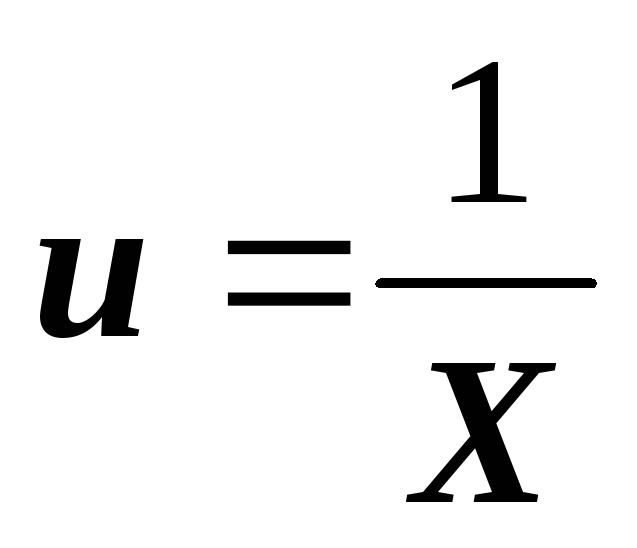
,we get the desired function X(t)
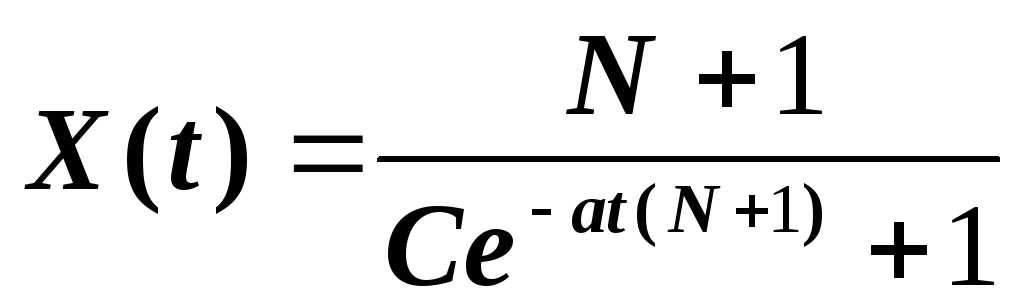
Since for t = 0 the value X (t) = 1, then to determine the quantity, we have the equation
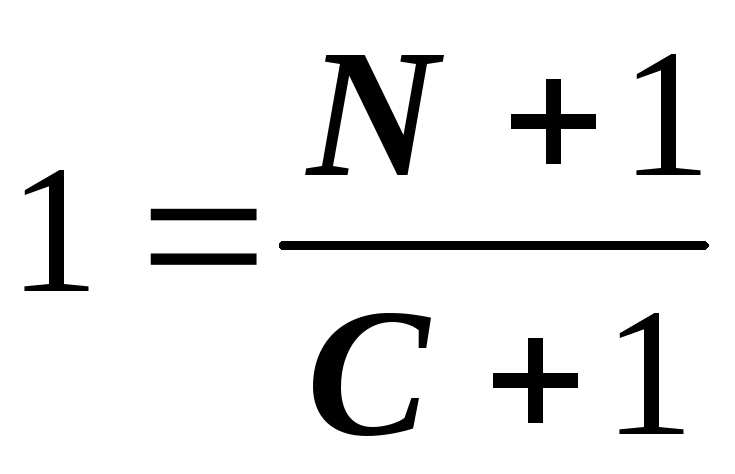
whence C = N
We finally get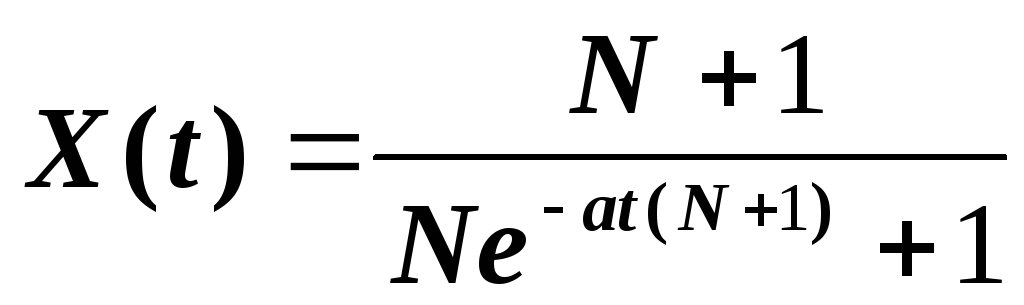
So, we know the number of cases as a function of time. We analyze the resulting formula. As t increases, the denominator of the fraction decreases, i.e., X (t) increases. This is consistent with our ideas, since, according to them, the number of cases can only increase.
It is interesting to find out how the rate of increase in the number of patients changes. To solve this problem, we need to study the value
Differentiating, we obtain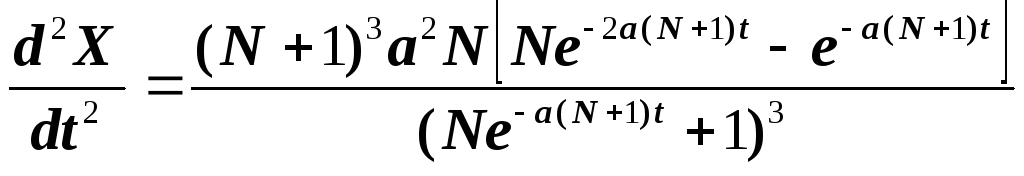
The fraction numerator vanishes at or turns into zero at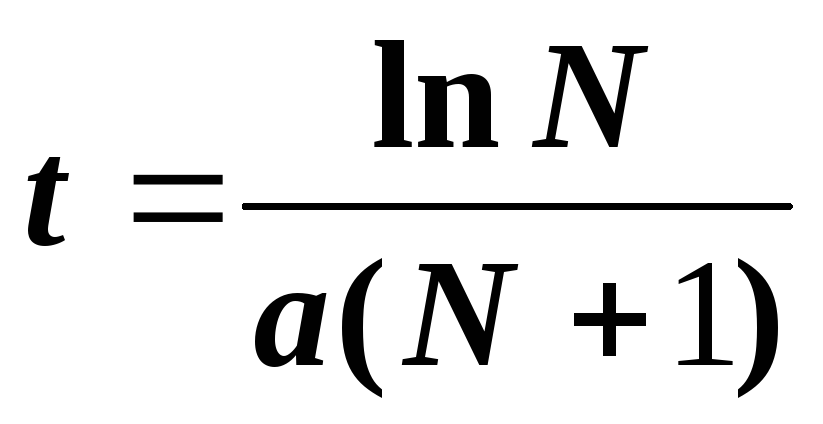
So when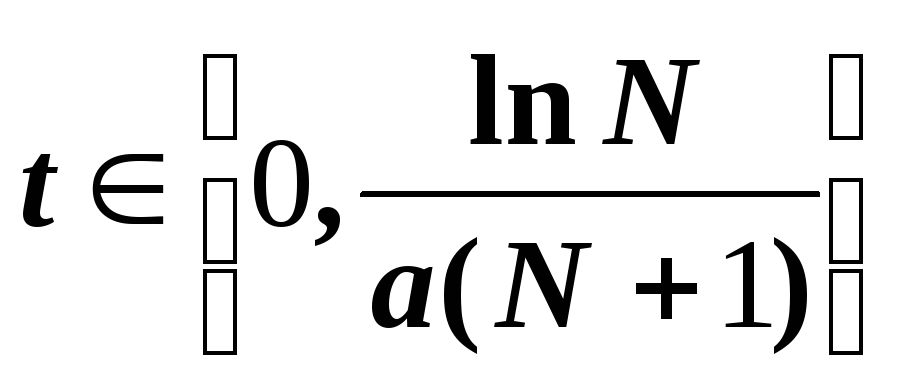
variable is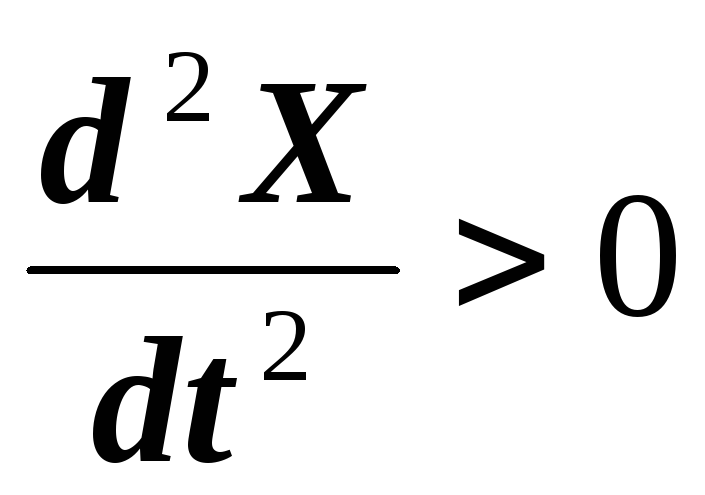
, and when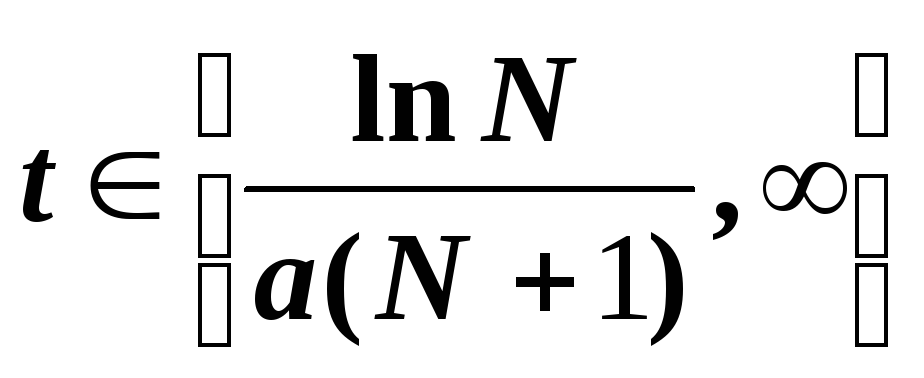
, variable is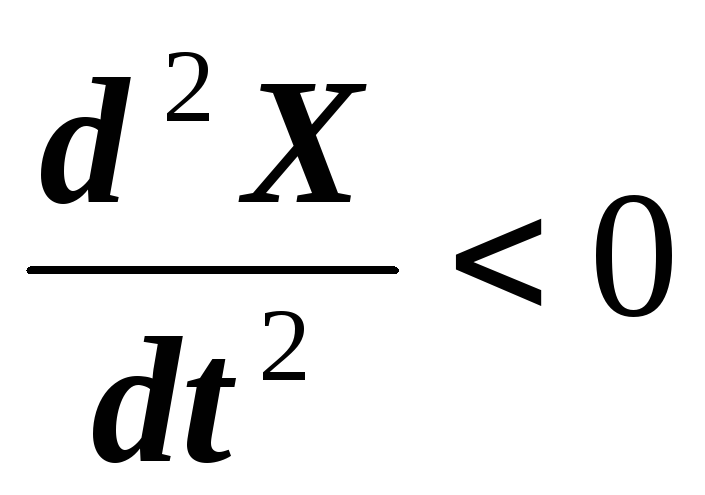
.
Therefore, the function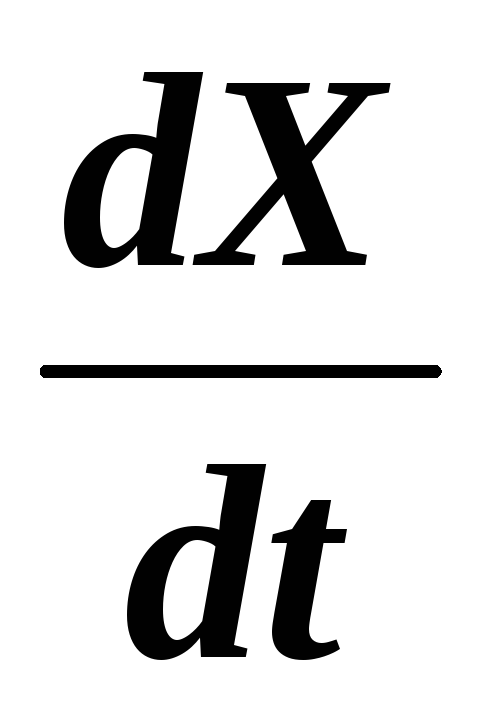
- the rate of increase in the number of cases - grows up to the moment
, and then decreases.
This result is in good agreement with experimental data sets, since it is known that at the beginning of the epidemic the number of cases increases sharply, and subsequently the spread of infection decreases.
Amateur translation
First St. Petersburg State Medical University named after I.P. Pavlov
https://studfile.net/preview/5845326/page:13/
Over the past many years of human existence, a huge number of people have died from various epidemics. Plague, cholera, flu, etc. often affected a significant mass of people. In order to be able to deal with epidemics, i.e. timely use of certain medical measures (quarantines, vaccinations, etc.), it is necessary to be able to compare the effectiveness of these measures. They can only be compared if it is possible to predict how the course of the epidemic will change during a given event, i.e. how the number of cases will change.
Hence, the need arises to build a model that could serve the purpose of the forecast.
For simplicity, we consider the natural course of the epidemic without any intervention and try to predict the consequences.
Since our goal is only to create an illustrative model, here we abstract from very many factors (conditions for the reproduction of bacterial cells, the degree of susceptibility to infection of individuals, the probability of meeting the carrier of infection with a healthy person, etc.)
So, let there be N healthy people, and at time t = 0 one sick person falls into this group - the source of infection. We will assume that no removal of patients from the group occurs. We also believe that a person becomes a source of infection immediately after he becomes infected.
Suppose at some point in time t
X (t) is the number of sources of infection,
Y (t) - the number of people who can get sick,
Then we have X (t) + Y (t) = N + 1 at any time.
For t = 0, the condition X (0) = 1
The number of new dX patients that appeared over the period of time dt will be proportional to the number of meetings of healthy and sick people, i.e. product of XY quantities. Therefore, you can write
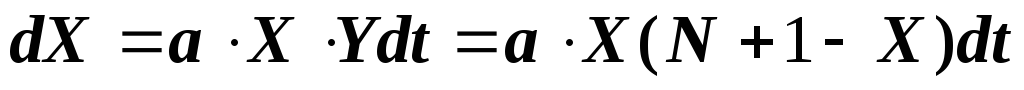
or
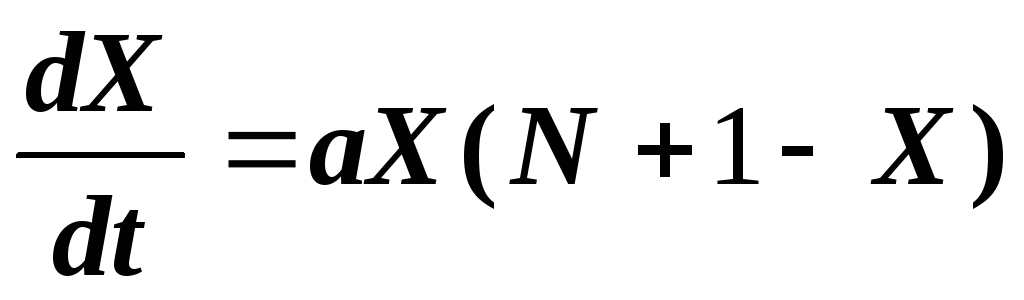
where a is the coefficient of proportionality.
The resulting differential equation together with the condition X (0) = 1 determines the function X (t), i.e. the number of cases at time t.
We find a general solution, after separating the variables.
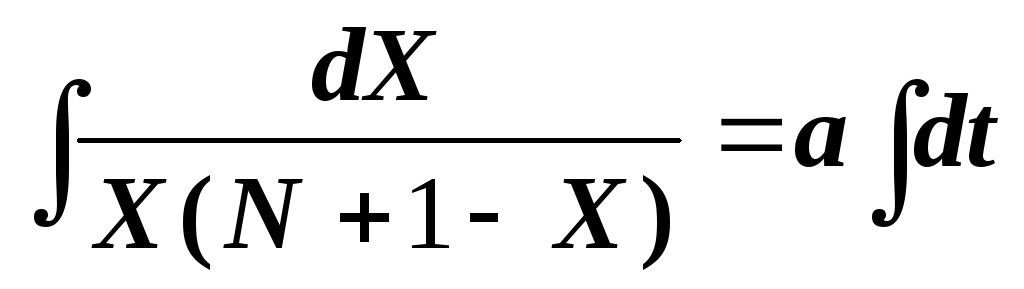
To take the first integral, divide the numerator and denominator of the fraction by

and introduce a new variable

, then
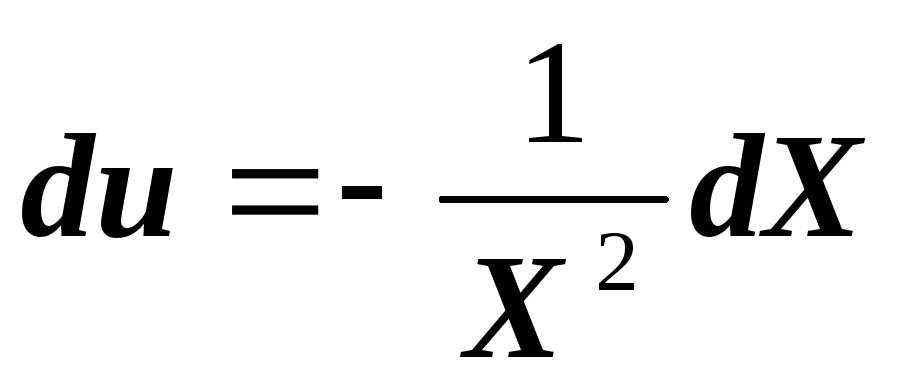
,.and from here
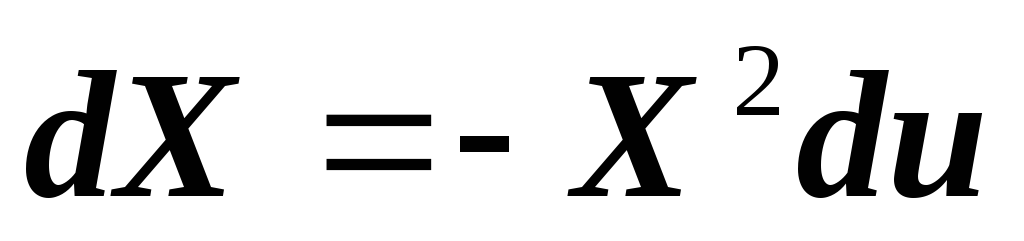
.
We replace the variable under the integral, and we obtain

After integration, we have
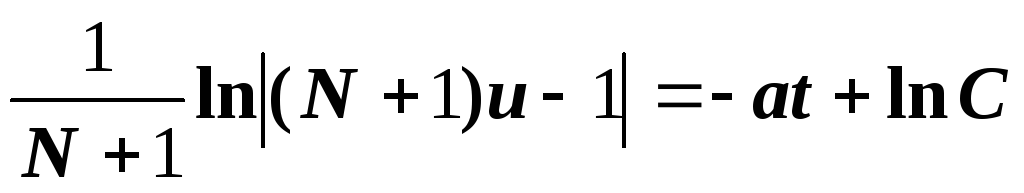
and therefore
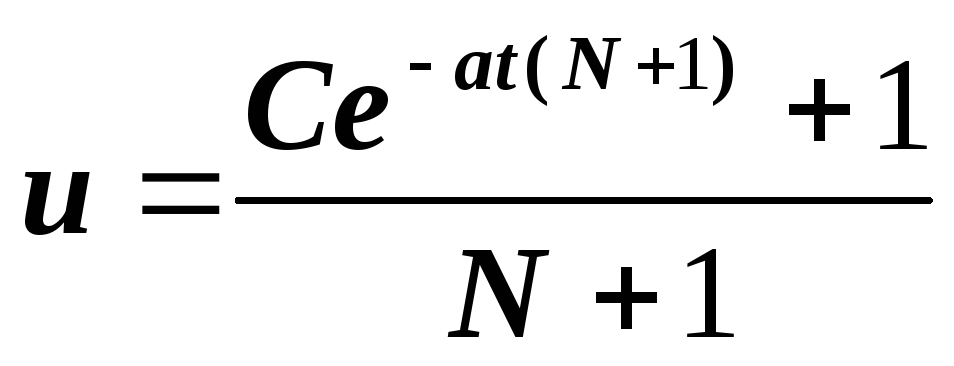
Given the fact that
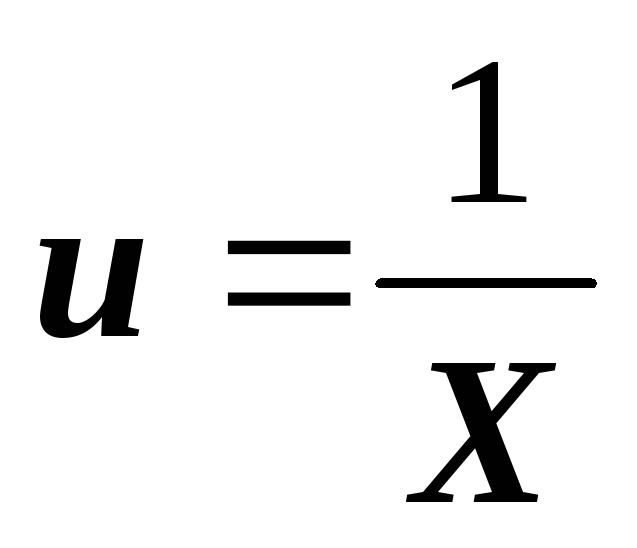
,we get the desired function X(t)
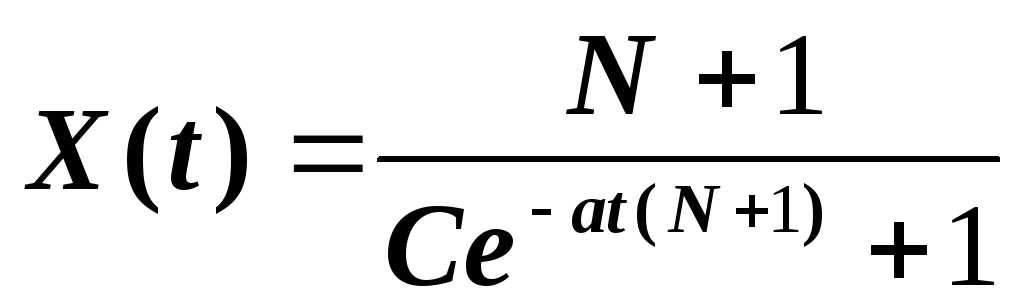
Since for t = 0 the value X (t) = 1, then to determine the quantity, we have the equation
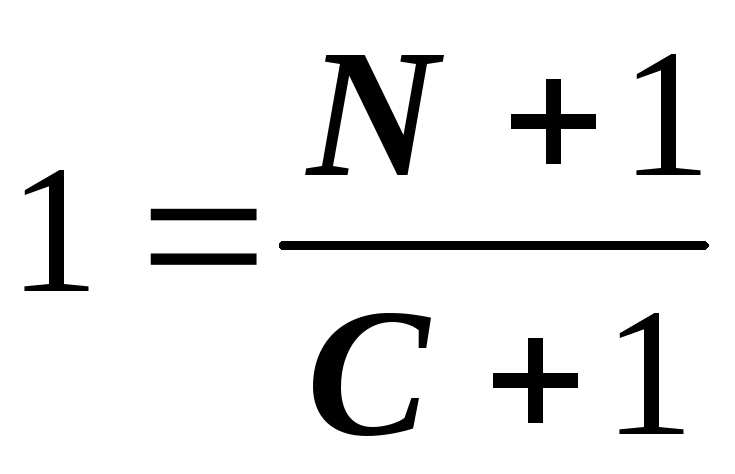
whence C = N
We finally get
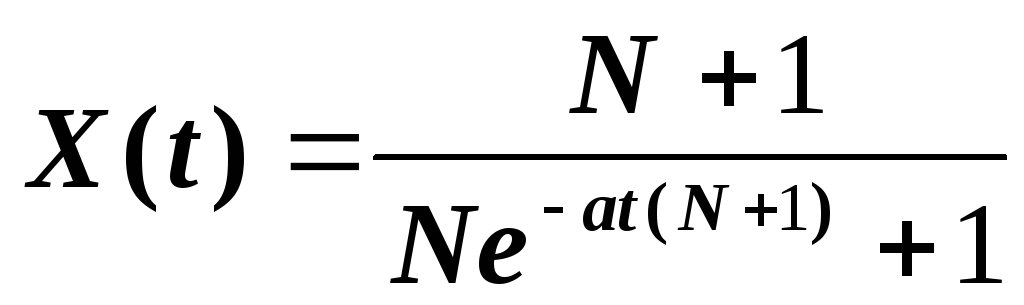
So, we know the number of cases as a function of time. We analyze the resulting formula. As t increases, the denominator of the fraction decreases, i.e., X (t) increases. This is consistent with our ideas, since, according to them, the number of cases can only increase.
It is interesting to find out how the rate of increase in the number of patients changes. To solve this problem, we need to study the value

Differentiating, we obtain
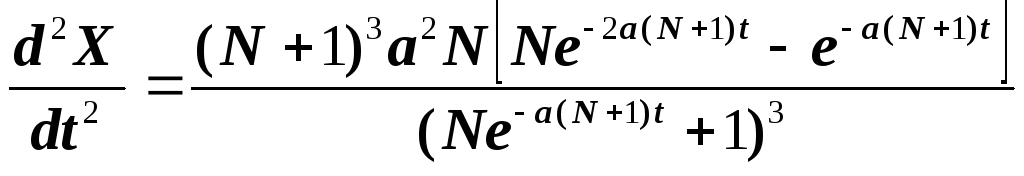
The fraction numerator vanishes at or turns into zero at
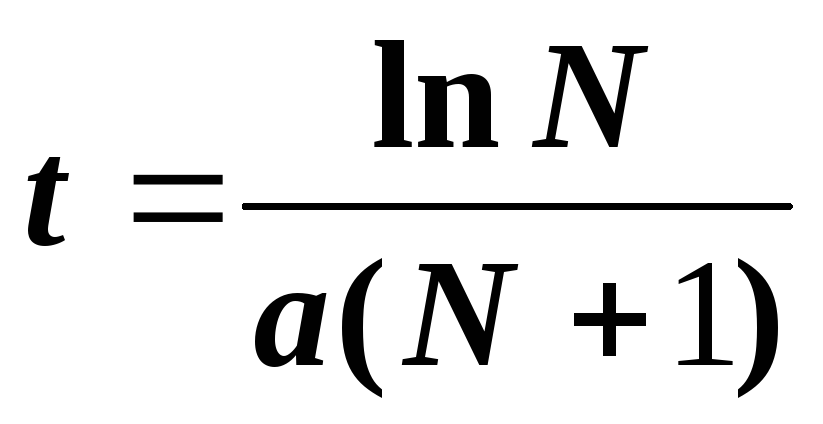
So when
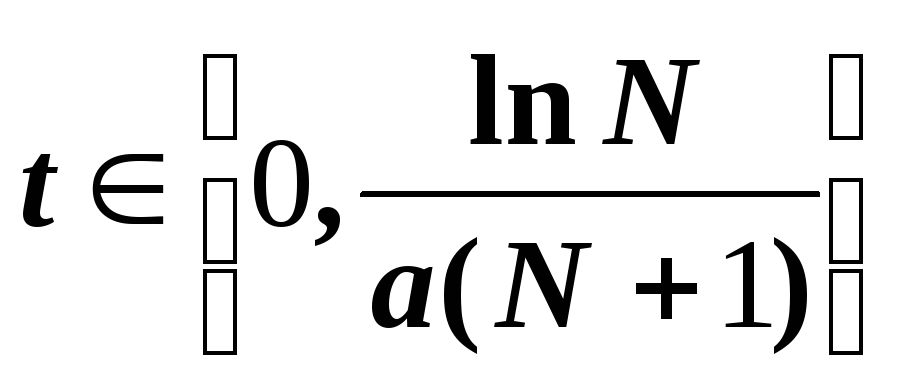
variable is
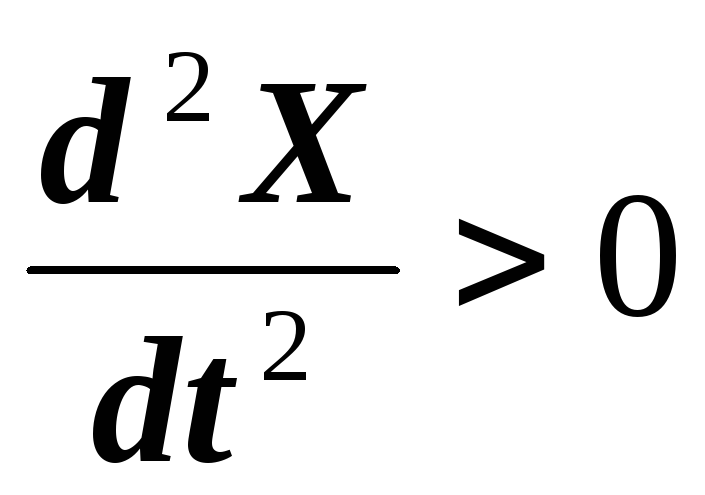
, and when
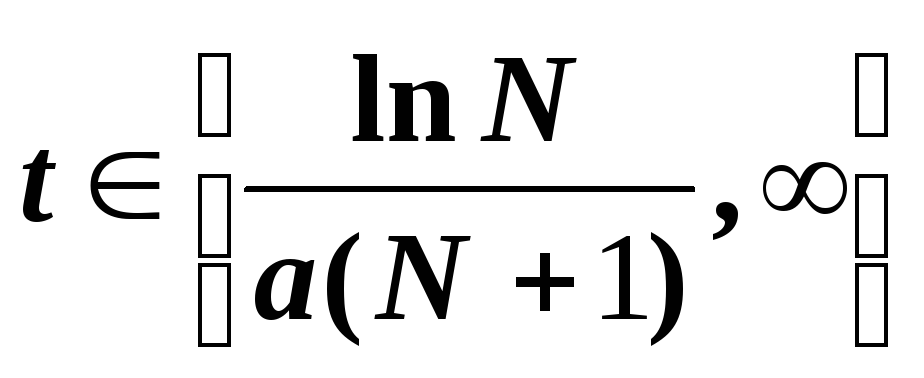
, variable is
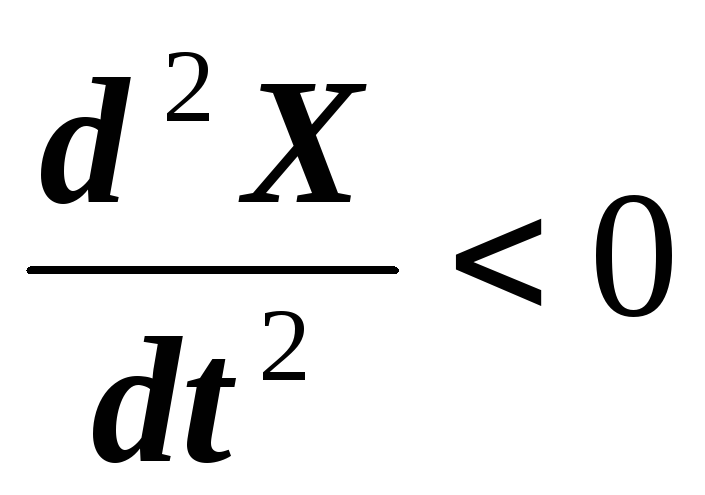
.
Therefore, the function
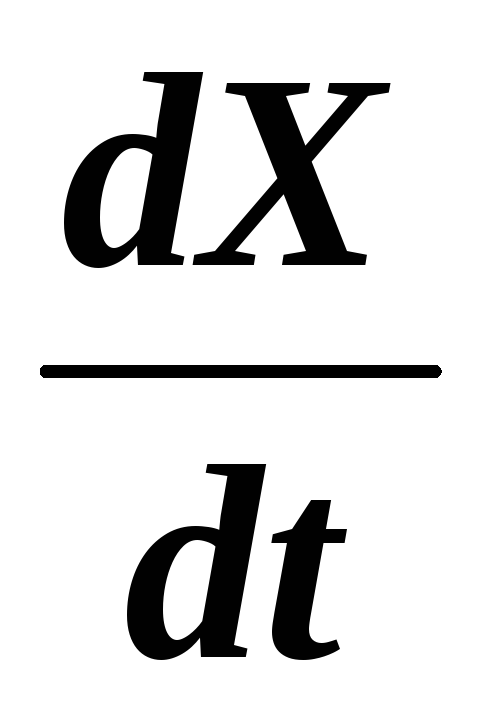
- the rate of increase in the number of cases - grows up to the moment

, and then decreases.
This result is in good agreement with experimental data sets, since it is known that at the beginning of the epidemic the number of cases increases sharply, and subsequently the spread of infection decreases.