Кого больше красивых девушек или клевых парней?
Много моих друзей говорят, что ебабельных девушек мало. Да, это так! Но для этих ебабельных девушек ебабельных парней еще меньше. freud_msk говорит, что на одну красивую девушку приходиться несколько клевых парней. Это не так. Счас я докажу совершенно обратное. Я использую математику, но не буду ей особо грузить. Там все просто будет.
Это продолжение статьи alex_odessa: "Чем красивее девушка тем меньше у нее выбор". Если вы ее не читали - прочитайте. Для самых ленивых приведу ее смысл: "Люди в основной своей массе среднячок. Для редких уродин и редких красавиц сложно найти пару своего уровня, поскольку очень отстойных и реально клевых парней тоже мало. Но клевым парням не особое западло переспать с девушкой похуже уровнем, поэтому красивые девушки сосут с еще большим проглотом. Чем красивее девушка тем меньше у нее выбор, есть только его иллюзия для окружающий".
Алекс психолог, а не математик, и не описал одну вещь. Я все время хотел продолжить статью, усилив ее выводы. Но у меня не хватало времени и сил, чтобы описать простой с точки зрения математики вывод понятным человеческим языком.
Нормальное распределение
В природе есть один закон, который выполняется везде. Это не законы физики, которые разные в квантовой механике и в теории относительности. Более того этот закон работает везде даже если это связанно с человеком или со свободным рынком или еще чем-то. Это не законы Гегеля он гараздо более объективен. Этот закон интуитивно понимает большинство людей в отдельных ситуациях, но не смотря на это он малоизвестен.
Это закон нормального распределения. Если какае-то величина зависит от двух параметров, то средних ее значений будет больше. Звучит туманно, но я счас все разжую.
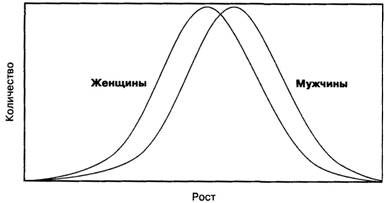
Людей ростом в 2 метра и 1.40 намного меньше чем людей ростом в 1.70. Среднячка больше всего.
Рост человека зависит от нескольких генов, поэтому он подвержен нормальному распределению.
Если взять распределение размеров члена, массы звезд, доходов населения, скорости движения молекулы ... то эти графики будут выглядеть также.
Возьмем одну игральную кость. Вероятность выпадение единицы 1/6, двойки тоже 1/6 ... Здесь мы видем равномерное распределения, нормальность распределения появляется когда добавим еще одну кость и просуммируем их результат.
Две кости могут выпасть в 6 * 6 = 36 комбинациях.
Сумма 2 может выпасть только когда на обеих костях выпало по единице (1+1=2). Вероятность 1/36
Для краткости и наглядности запишем это так
2: 1+1 == 1/36
3: 2+1; 1+2 ==2/36
4 2+2; 3+1; 1+3 == 3/36
5 2+3; 3+2; 1+4; 4+1 == 4/36
6 3+3; 5+1; 1+5; 2+4; 4+2 == 5/36
7: 1+6; 6+1; 5+2; 2+5; 3+4; 4+3 == 6/36
8. 4+4, 5+3, 3+5, 2+6, 6+2 == 5/36
9. 5+4, 4+5, 6+3, 3+6 == 4/36
10. 5+5, 4+6, 6+4 == 3/36
11. 6+5, 5+6 == 2/36
12. 6+6 = 1/36
Легко видеть пирамидку. Среднячка намного больше. Вы можете перевернуть эту пирамидку на 90 градусов и увидеть совпадение с прошлым графиком человеческого роста.
Кстати, вы можете проверить мои выкладки просто просуммировав вероятности, вы получите 36/36
Если добавить еще одну кость то среднячок будет еще более вероятен чем максимум и минимум.
Для минимума сумма 3, только 1+1+1 ==== 1 комбинация
Для среднячка сумма 11=1+5+5, 5+1+5, 5+5+1, 2+5+4, 2+ 4+5, 5+2+4, 4+2+5 ... итак далее всего 26 комбинаций.
Смотрите добавили всего одну кость, а дифференциация выросла с 1 к 6 до 1 к 26!!!
Короче, чем больше костей тем больше выражен характер нормального распределения. Т.е. от чем большего числа параметров зависит случайная величина, тем больше среднячка и меньше минимумов и максимумов.
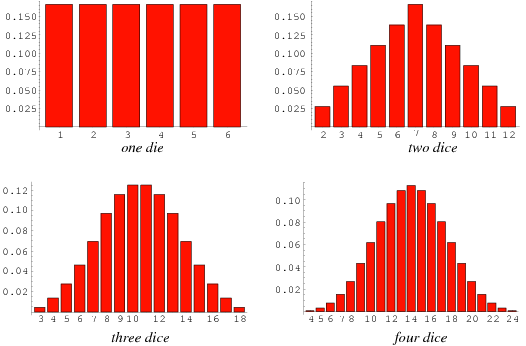
Чем больше параметров, тем больше прослеживаться среднячок.
К чему я клоню? Ценность девушки почти полностью исчерпывается ее красотой. Есть и другие параметры но они не так сильно учитываются, как у мужчин. Ценность мужчины учитывает внешность и еще кучу параметров. Если брать Т100б их 5, если брать ЛасВегас, их 7. Я не приверженец ни одной из этих теорий. Просто утверждаю ценность мужчины зависит не только от его внешности. Другие параметры ценности имеют тоже нормальное распределение (интеллект, самоуверенность, статус).
Клевых челов намного меньше, чем красивых девушек.
Более жизненный пример:
Например, есть гипотетический сайт знакомств. Он пиздец какой умный. Умеет оценивать параметры мужчин красоту, ум, статус, рост, уверенность в себе и еще кучу всего и искать по ним. Девушка вбивает красивее среднего ей высырается 1000 вариантов. Затем добавляет еще одно условие "рост выше среднего" выводиться 500 парней. Так задает еще пару условий и остается всего парочку вариантов. Очевидно, что чем больше условий она вобьет тем меньше вариантов у нее останется. Если у нее высокая самооценка (как у большинства красивых девушек), то она вобъет много условий.
Чел обычно вобьет только красоту и у него выведется намного больше вариантов чем у девушки. Если чел клевый, то большинство девушек согласятся с ним встретиться. Причем для большинства красивых девушек он будет если не единственным, то одним из немногих, а для него вариантов будет в разы, в десятки раз, больше!!!
Для чисто формального Математического доказательства необходимы следующие допущения:
1. Доминирующий параметр в ценности девушки красота.
2. Красота в ценности мужчины не является доминирующий параметром или доминирует слабее.
3. В ценности мужчины существует хотя-бы два слабозависимых параметра. Например, ум не сильно зависит от красоты.
4. Зависимость от этих двух параметров на интересующем нам диапазоне (условно от 6 до 9 балов) близка к линейной. В Т100б и ЛасВегасе это так. Без этого условия тоже можно доказать, но мой аппарат тервера исчерпывается Центральной предельной теоремой и законом больших чисел. В принципе, достаточно чтобы функция если зафиксировать все остальные была монотонной (либо всегда увеличивалась либо всегда уменьшалась) по этим двум параметрам.
Алекс-Одесса на Адреналине рассказывал о следующем эксперименте. Есть класс или группа в универе и психологи попросили девушек и парней выбрать пару ебабельных вариантов. Симпатии мужчин распределились ровнее женщин т.е. даже страшки получали одну симпатию. А среди парней симпатию получили только несколько, но зато всех баб.
И это далеко не все
Теперь прибавим то что, что клевому парню не западло переспать с девушкой похуже или что он может всецело уйти в бизнес, искусство. Т.е. ему есть что делать, кроме как мутить с девушками своего уровня.
Еще нужно прибавить то, что к красивым девушкам реже подходят из-за страха, который наблюдается даже у самых клевых натуралов. Следствие закона Йоркса-Додсона, одного из 3ех фундаментальных законов психологии. Кстати кривая этого закона для сложных задач тоже имеет нормальное распределение.
Еще нужно прибавить то, что девушки не выбирают кто к ним подходит, а мужчины выбирают. Большинство мужчин не так часто подходят как мы. Т.е. число контактов с потенциально приемлемыми партнерами у нас выше. Причем в разы.
Если мелочиться, то можно прибавить еще то что по статистике на 10 девчонок, всего 9 ребят. Один из которых гомосек :)
Теперь представим на каком-то уровне телочек втрое больше чем парней. Т.е. на 6 телочек 2 парня. Половина парней встречается с кем-то. В нашем пример 2 парня, поэтому половина парней это один парень. Для удобства скажем что он встречается с девушкой своего уровня (хотя часто уровень ниже). Что мы получаем? Остается 5 свободных девушек и всего один парень! Т.е. телочек теперь не в 3, а в целых пять раз больше.
Что мы получаем?
Клевый чел в разы объективно ценнее девушки его же уровня. Чем клевее чел, тем это больше проявляется.
Это продолжение статьи alex_odessa: "Чем красивее девушка тем меньше у нее выбор". Если вы ее не читали - прочитайте. Для самых ленивых приведу ее смысл: "Люди в основной своей массе среднячок. Для редких уродин и редких красавиц сложно найти пару своего уровня, поскольку очень отстойных и реально клевых парней тоже мало. Но клевым парням не особое западло переспать с девушкой похуже уровнем, поэтому красивые девушки сосут с еще большим проглотом. Чем красивее девушка тем меньше у нее выбор, есть только его иллюзия для окружающий".
Алекс психолог, а не математик, и не описал одну вещь. Я все время хотел продолжить статью, усилив ее выводы. Но у меня не хватало времени и сил, чтобы описать простой с точки зрения математики вывод понятным человеческим языком.
Нормальное распределение
В природе есть один закон, который выполняется везде. Это не законы физики, которые разные в квантовой механике и в теории относительности. Более того этот закон работает везде даже если это связанно с человеком или со свободным рынком или еще чем-то. Это не законы Гегеля он гараздо более объективен. Этот закон интуитивно понимает большинство людей в отдельных ситуациях, но не смотря на это он малоизвестен.
Это закон нормального распределения. Если какае-то величина зависит от двух параметров, то средних ее значений будет больше. Звучит туманно, но я счас все разжую.

Людей ростом в 2 метра и 1.40 намного меньше чем людей ростом в 1.70. Среднячка больше всего.
Рост человека зависит от нескольких генов, поэтому он подвержен нормальному распределению.
Если взять распределение размеров члена, массы звезд, доходов населения, скорости движения молекулы ... то эти графики будут выглядеть также.
Возьмем одну игральную кость. Вероятность выпадение единицы 1/6, двойки тоже 1/6 ... Здесь мы видем равномерное распределения, нормальность распределения появляется когда добавим еще одну кость и просуммируем их результат.
Две кости могут выпасть в 6 * 6 = 36 комбинациях.
Сумма 2 может выпасть только когда на обеих костях выпало по единице (1+1=2). Вероятность 1/36
Для краткости и наглядности запишем это так
2: 1+1 == 1/36
3: 2+1; 1+2 ==2/36
4 2+2; 3+1; 1+3 == 3/36
5 2+3; 3+2; 1+4; 4+1 == 4/36
6 3+3; 5+1; 1+5; 2+4; 4+2 == 5/36
7: 1+6; 6+1; 5+2; 2+5; 3+4; 4+3 == 6/36
8. 4+4, 5+3, 3+5, 2+6, 6+2 == 5/36
9. 5+4, 4+5, 6+3, 3+6 == 4/36
10. 5+5, 4+6, 6+4 == 3/36
11. 6+5, 5+6 == 2/36
12. 6+6 = 1/36
Легко видеть пирамидку. Среднячка намного больше. Вы можете перевернуть эту пирамидку на 90 градусов и увидеть совпадение с прошлым графиком человеческого роста.
Кстати, вы можете проверить мои выкладки просто просуммировав вероятности, вы получите 36/36
Если добавить еще одну кость то среднячок будет еще более вероятен чем максимум и минимум.
Для минимума сумма 3, только 1+1+1 ==== 1 комбинация
Для среднячка сумма 11=1+5+5, 5+1+5, 5+5+1, 2+5+4, 2+ 4+5, 5+2+4, 4+2+5 ... итак далее всего 26 комбинаций.
Смотрите добавили всего одну кость, а дифференциация выросла с 1 к 6 до 1 к 26!!!
Короче, чем больше костей тем больше выражен характер нормального распределения. Т.е. от чем большего числа параметров зависит случайная величина, тем больше среднячка и меньше минимумов и максимумов.

Чем больше параметров, тем больше прослеживаться среднячок.
К чему я клоню? Ценность девушки почти полностью исчерпывается ее красотой. Есть и другие параметры но они не так сильно учитываются, как у мужчин. Ценность мужчины учитывает внешность и еще кучу параметров. Если брать Т100б их 5, если брать ЛасВегас, их 7. Я не приверженец ни одной из этих теорий. Просто утверждаю ценность мужчины зависит не только от его внешности. Другие параметры ценности имеют тоже нормальное распределение (интеллект, самоуверенность, статус).
Клевых челов намного меньше, чем красивых девушек.
Более жизненный пример:
Например, есть гипотетический сайт знакомств. Он пиздец какой умный. Умеет оценивать параметры мужчин красоту, ум, статус, рост, уверенность в себе и еще кучу всего и искать по ним. Девушка вбивает красивее среднего ей высырается 1000 вариантов. Затем добавляет еще одно условие "рост выше среднего" выводиться 500 парней. Так задает еще пару условий и остается всего парочку вариантов. Очевидно, что чем больше условий она вобьет тем меньше вариантов у нее останется. Если у нее высокая самооценка (как у большинства красивых девушек), то она вобъет много условий.
Чел обычно вобьет только красоту и у него выведется намного больше вариантов чем у девушки. Если чел клевый, то большинство девушек согласятся с ним встретиться. Причем для большинства красивых девушек он будет если не единственным, то одним из немногих, а для него вариантов будет в разы, в десятки раз, больше!!!
Для чисто формального Математического доказательства необходимы следующие допущения:
1. Доминирующий параметр в ценности девушки красота.
2. Красота в ценности мужчины не является доминирующий параметром или доминирует слабее.
3. В ценности мужчины существует хотя-бы два слабозависимых параметра. Например, ум не сильно зависит от красоты.
4. Зависимость от этих двух параметров на интересующем нам диапазоне (условно от 6 до 9 балов) близка к линейной. В Т100б и ЛасВегасе это так. Без этого условия тоже можно доказать, но мой аппарат тервера исчерпывается Центральной предельной теоремой и законом больших чисел. В принципе, достаточно чтобы функция если зафиксировать все остальные была монотонной (либо всегда увеличивалась либо всегда уменьшалась) по этим двум параметрам.
Алекс-Одесса на Адреналине рассказывал о следующем эксперименте. Есть класс или группа в универе и психологи попросили девушек и парней выбрать пару ебабельных вариантов. Симпатии мужчин распределились ровнее женщин т.е. даже страшки получали одну симпатию. А среди парней симпатию получили только несколько, но зато всех баб.
И это далеко не все
Теперь прибавим то что, что клевому парню не западло переспать с девушкой похуже или что он может всецело уйти в бизнес, искусство. Т.е. ему есть что делать, кроме как мутить с девушками своего уровня.
Еще нужно прибавить то, что к красивым девушкам реже подходят из-за страха, который наблюдается даже у самых клевых натуралов. Следствие закона Йоркса-Додсона, одного из 3ех фундаментальных законов психологии. Кстати кривая этого закона для сложных задач тоже имеет нормальное распределение.
Еще нужно прибавить то, что девушки не выбирают кто к ним подходит, а мужчины выбирают. Большинство мужчин не так часто подходят как мы. Т.е. число контактов с потенциально приемлемыми партнерами у нас выше. Причем в разы.
Если мелочиться, то можно прибавить еще то что по статистике на 10 девчонок, всего 9 ребят. Один из которых гомосек :)
Теперь представим на каком-то уровне телочек втрое больше чем парней. Т.е. на 6 телочек 2 парня. Половина парней встречается с кем-то. В нашем пример 2 парня, поэтому половина парней это один парень. Для удобства скажем что он встречается с девушкой своего уровня (хотя часто уровень ниже). Что мы получаем? Остается 5 свободных девушек и всего один парень! Т.е. телочек теперь не в 3, а в целых пять раз больше.
Что мы получаем?
Клевый чел в разы объективно ценнее девушки его же уровня. Чем клевее чел, тем это больше проявляется.