Загадка мироздание, универсальное математическое дерево
Википедия: Дерево Пифагора

Дерево Пифагора - разновидность фрактала, основанная на фигуре, известной как «Пифагоровы штаны».
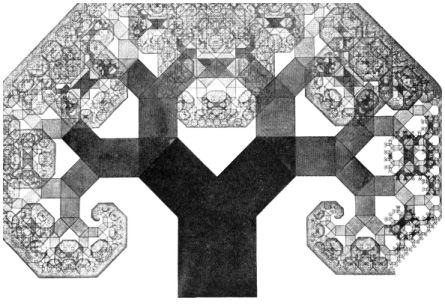
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. Впервые дерево Пифагора построил А. Е. Босман во время Второй мировой войны, используя обычную чертёжную линейку.
Старался во времья войны в оккупированной Голландии он не зря:


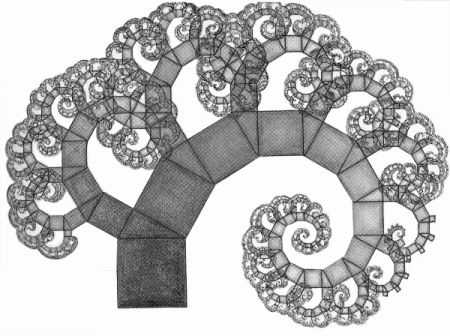
Дерево Пифагора под углом:

А карандашом автора этого дерева даже более красиво. У них явно война была по спокойнее:
На неё очень похожя кривая Леви: Кривая Леви
А вот 2Д фракталы, созданые с итерацией некой простой формулы, на Ultrafractal:
(тип ducks, ducky, kaliset)

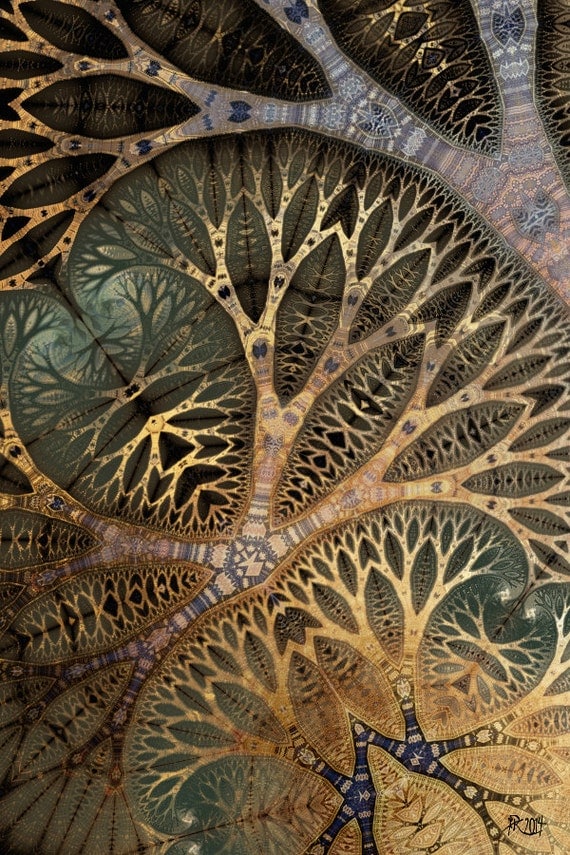

Переходим на 3Д и программу Mandelbulb3D. И тоже самое, только создано при помошю совсем иной формулы, если не ошибаюсь, складывающей пространство. Видоизменноный куб Менгера:

А вот впринципе то же дерево, только от другой формулы, amazing surface. Тут пространство складывается и так же поворачивается вокруг оси.

Еще одно дерево, навернека сгенерированное еще иным, самым простым способом, "Fractal canopy":

По сути они все похожи:

Навернека это означает, что эта фигура является фундаментальной. И тут видна характеристика универсальность, похожее дерево получается разными методами, а так же в разных дименсиях. Множество Мандельброта обладает свойством универсальности только в 2Д. А 3Д Мандельброт Ит-ешники искали, искали но так и не нашли.
А на природе
В умеренном поясе тольки ивы растут таким же способом. У берёз имеется главная вертикальная ветка. У ив же всегда последная почка на ветке отмирает. И весной новая поросль начинает расти со сторонней почки.
Больше всего на эти математические деревца похожа разновидность ив Salix Fragilis Bullata или Ива Ломкая Шаровидная:


Тут вопрос, а почему одна и та же форма появляется в куче разных фракталов. Имеет ли это какую то математическую причину? Является ли оно какой то универсальной и фундаментальной фигурой, наподобии треугольник (наверное да). Для дерева же это возможно просто самый эффективный метод роста, самоподерживаемый и самосохраняющийсья. Чтоб получилось такое вот дерево оно не должно обладать огромной регуляторной генетической машинерией. И маленькие веточки не должны знать, где они находится на дереве. Фракталы самоподобны, и это обеспечивает самой простой и экономный вариант роста.
Следовательно, на других планетах тоже может быть деревья, и они будут похожими. Так как математические закономерности везде одинаковы.
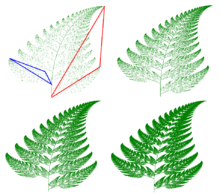
На других планетах даже могут попадаться папоротники, как этот не универсальный но математический Папоротник Барнсли:
п.с.
Пока искал про фракталов, нашёл какую то научную статью про фрактальность. Нечего не понял, математика особый язык. Но что примечательно, статья иранских учёных. И в сети частенько наталкиваюсь на статьи Иранских учёных, не так часто как на американских, но таки. Они далеко не дикари.
https://arxiv.org/pdf/1511.01330v1.pdf
Дерево Пифагора - разновидность фрактала, основанная на фигуре, известной как «Пифагоровы штаны».
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. Впервые дерево Пифагора построил А. Е. Босман во время Второй мировой войны, используя обычную чертёжную линейку.
Старался во времья войны в оккупированной Голландии он не зря:

Дерево Пифагора под углом:

А карандашом автора этого дерева даже более красиво. У них явно война была по спокойнее:


На неё очень похожя кривая Леви: Кривая Леви
А вот 2Д фракталы, созданые с итерацией некой простой формулы, на Ultrafractal:
(тип ducks, ducky, kaliset)



Переходим на 3Д и программу Mandelbulb3D. И тоже самое, только создано при помошю совсем иной формулы, если не ошибаюсь, складывающей пространство. Видоизменноный куб Менгера:

А вот впринципе то же дерево, только от другой формулы, amazing surface. Тут пространство складывается и так же поворачивается вокруг оси.

Еще одно дерево, навернека сгенерированное еще иным, самым простым способом, "Fractal canopy":

По сути они все похожи:
Навернека это означает, что эта фигура является фундаментальной. И тут видна характеристика универсальность, похожее дерево получается разными методами, а так же в разных дименсиях. Множество Мандельброта обладает свойством универсальности только в 2Д. А 3Д Мандельброт Ит-ешники искали, искали но так и не нашли.
А на природе
В умеренном поясе тольки ивы растут таким же способом. У берёз имеется главная вертикальная ветка. У ив же всегда последная почка на ветке отмирает. И весной новая поросль начинает расти со сторонней почки.
Больше всего на эти математические деревца похожа разновидность ив Salix Fragilis Bullata или Ива Ломкая Шаровидная:


Тут вопрос, а почему одна и та же форма появляется в куче разных фракталов. Имеет ли это какую то математическую причину? Является ли оно какой то универсальной и фундаментальной фигурой, наподобии треугольник (наверное да). Для дерева же это возможно просто самый эффективный метод роста, самоподерживаемый и самосохраняющийсья. Чтоб получилось такое вот дерево оно не должно обладать огромной регуляторной генетической машинерией. И маленькие веточки не должны знать, где они находится на дереве. Фракталы самоподобны, и это обеспечивает самой простой и экономный вариант роста.
Следовательно, на других планетах тоже может быть деревья, и они будут похожими. Так как математические закономерности везде одинаковы.
На других планетах даже могут попадаться папоротники, как этот не универсальный но математический Папоротник Барнсли:

п.с.
Пока искал про фракталов, нашёл какую то научную статью про фрактальность. Нечего не понял, математика особый язык. Но что примечательно, статья иранских учёных. И в сети частенько наталкиваюсь на статьи Иранских учёных, не так часто как на американских, но таки. Они далеко не дикари.
https://arxiv.org/pdf/1511.01330v1.pdf