Kurtosis & Skew
В продолжение вот этого поста.
Итак, как принято измерять разницу между "mystery" distribution и normal one? Для этого придумали два параметра: Kurtosis & Skew.
KURTOSIS
A high kurtosis distribution has a sharper "peak" and flatter "tails", while a low kurtosis distribution has a more rounded peak with wider "shoulders".
Distributions with zero kurtosis are called mesokurtic, or mesokurtotic. The most prominent example of a mesokurtic distribution is the normal distribution family, regardless of the values of its parameters.
A distribution with positive kurtosis is called leptokurtic, or leptokurtotic. In terms of shape, a leptokurtic distribution has a more acute "peak" around the mean (that is, a higher probability than a normally distributed variable of values near the mean) and "fat tails" (that is, a higher probability than a normally distributed variable of extreme values). Examples of leptokurtic distributions include the Laplace distribution and the logistic distribution. Such distributions are sometimes termed "super Gaussian".
A distribution with negative kurtosis is called platykurtic, or platykurtotic. In terms of shape, a platykurtic distribution has a smaller "peak" around the mean (that is, a lower probability than a normally distributed variable of values near the mean) and "thin tails" (that is, a lower probability than a normally distributed variable of extreme values). Examples of platykurtic distributions include the continuous or discrete uniform distributions, and the raised cosine distribution. The most platykurtic distribution of all is the Bernoulli distribution with p = ½ (for example the number of times one obtains "heads" when flipping a coin once), for which the kurtosis is -2. Such distributions are sometimes termed "sub Gaussian".
SKEW
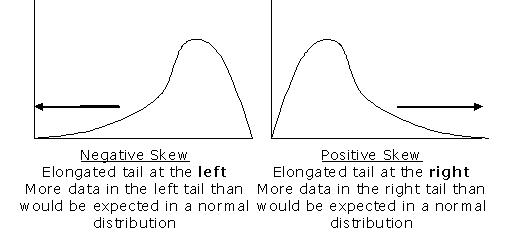
Consider the distribution in the figure. The bars on the right side of the distribution taper differently than the bars on the left side. These tapering sides are called tails (or snakes), and they provide a visual means for determining which of the two kinds of skewness a distribution has:
1. positive skew: The right tail is longer; the mass of the distribution is concentrated on the left of the figure. The distribution is said to be right-skewed.
2. negative skew: The left tail is longer; the mass of the distribution is concentrated on the right of the figure. The distribution is said to be left-skewed.
Source:
http://en.wikipedia.org/wiki/Kurtosis
http://en.wikipedia.org/wiki/Kurtosis_risk
http://en.wikipedia.org/wiki/Skewness
http://en.wikipedia.org/wiki/Skewness_risk
А также excel файлик, позволяющий построить распределение для конкретной акции по историческим данным и измерить Kurt&Skew.
PS. Все, тему распределений считаю для себя раскрытой.
Итак, как принято измерять разницу между "mystery" distribution и normal one? Для этого придумали два параметра: Kurtosis & Skew.
KURTOSIS
A high kurtosis distribution has a sharper "peak" and flatter "tails", while a low kurtosis distribution has a more rounded peak with wider "shoulders".
Distributions with zero kurtosis are called mesokurtic, or mesokurtotic. The most prominent example of a mesokurtic distribution is the normal distribution family, regardless of the values of its parameters.
A distribution with positive kurtosis is called leptokurtic, or leptokurtotic. In terms of shape, a leptokurtic distribution has a more acute "peak" around the mean (that is, a higher probability than a normally distributed variable of values near the mean) and "fat tails" (that is, a higher probability than a normally distributed variable of extreme values). Examples of leptokurtic distributions include the Laplace distribution and the logistic distribution. Such distributions are sometimes termed "super Gaussian".
A distribution with negative kurtosis is called platykurtic, or platykurtotic. In terms of shape, a platykurtic distribution has a smaller "peak" around the mean (that is, a lower probability than a normally distributed variable of values near the mean) and "thin tails" (that is, a lower probability than a normally distributed variable of extreme values). Examples of platykurtic distributions include the continuous or discrete uniform distributions, and the raised cosine distribution. The most platykurtic distribution of all is the Bernoulli distribution with p = ½ (for example the number of times one obtains "heads" when flipping a coin once), for which the kurtosis is -2. Such distributions are sometimes termed "sub Gaussian".
SKEW
Consider the distribution in the figure. The bars on the right side of the distribution taper differently than the bars on the left side. These tapering sides are called tails (or snakes), and they provide a visual means for determining which of the two kinds of skewness a distribution has:
1. positive skew: The right tail is longer; the mass of the distribution is concentrated on the left of the figure. The distribution is said to be right-skewed.
2. negative skew: The left tail is longer; the mass of the distribution is concentrated on the right of the figure. The distribution is said to be left-skewed.

Source:
http://en.wikipedia.org/wiki/Kurtosis
http://en.wikipedia.org/wiki/Kurtosis_risk
http://en.wikipedia.org/wiki/Skewness
http://en.wikipedia.org/wiki/Skewness_risk
А также excel файлик, позволяющий построить распределение для конкретной акции по историческим данным и измерить Kurt&Skew.
PS. Все, тему распределений считаю для себя раскрытой.